Der Stoff
Das Thema bezieht sich auf die Materialbearbeitung mit Laserstrahlen, das heißt, auf die Bearbeitung von Stoffen allgemein. Die beiden Bezeichnungen "Material" und "Stoff" werden im naturwissenschaftlichen und technischen Sprachgebrauch nebeneinander gleichbedeutend verwendet. Im Folgenden ist "Stoff" ausgewählt. Der Begriff Material und damit auch Stoff ist weitergehend als der Begriff Werkstoff. Der Titel Werkstoff-Bearbeitung würde den Inhalt auf Fertigungstechniken einschränken, das heißt, auf feste Stoffe mit Form und Gestalt, die bearbeitet werden. Das dazugehörende Fachgebiet, die Werkstoffkunde, wird in verschiedenen Lehrbüchern ausgezeichnet behandelt. [1]
Diese ist auch im Feld der Materialbearbeitung mit
Laserstrahlen eine wesentliche Grundlage. Der Übergang von
Werkstoff auf Material erweitert den Bereich, so dass auch
Anwendungen wie Sterilisation von Gewürzen, der Einsatz an
Menschen oder das Zertrümmern von Gesteinen mit wertvollem
Inhalt und auch das chemische Aktivieren von Prozessen in
Flüssigkeiten und Gasen einbezogen werden. Das Ganze ist
derart umfangreich, dass sich der Inhalt dieses Kapitels auf
den physikalisch-technischen Hintergrund der Kenntnisse von
Stoffen beschränkt. Daraus können dann
Bearbeitungsmöglichkeiten abgeschätzt und deren Grenzen für
die vorgesehenen Zwecke abgeleitet werden.
1 STOFFE
Zu Beginn eine kurze physikalische Beschreibung der
verschiedenen Stoffklassen aufgrund ihres atomaren Aufbaus.
Aus diesem werden einige Grundeigenschaften ersichtlich. Die
Atomkerne bestimmen wesentlich die Dichte und das Verhalten
bei Kernreaktionen, die Elektronenhülle bestimmt alle
anderen Eigenschaften, so den Aufbau und das Verhalten der
Stoffe während der Materialbearbeitung. Wesentlich dabei
sind die Bindungen, die aus den Atomen einen Stoff bilden.
Diese gliedern sich in vier verschiedene Arten, die
Grenzfälle darstellen: Drei starke (Primärbindungen) und
eine schwache (Sekundärbindung), Bild 1.
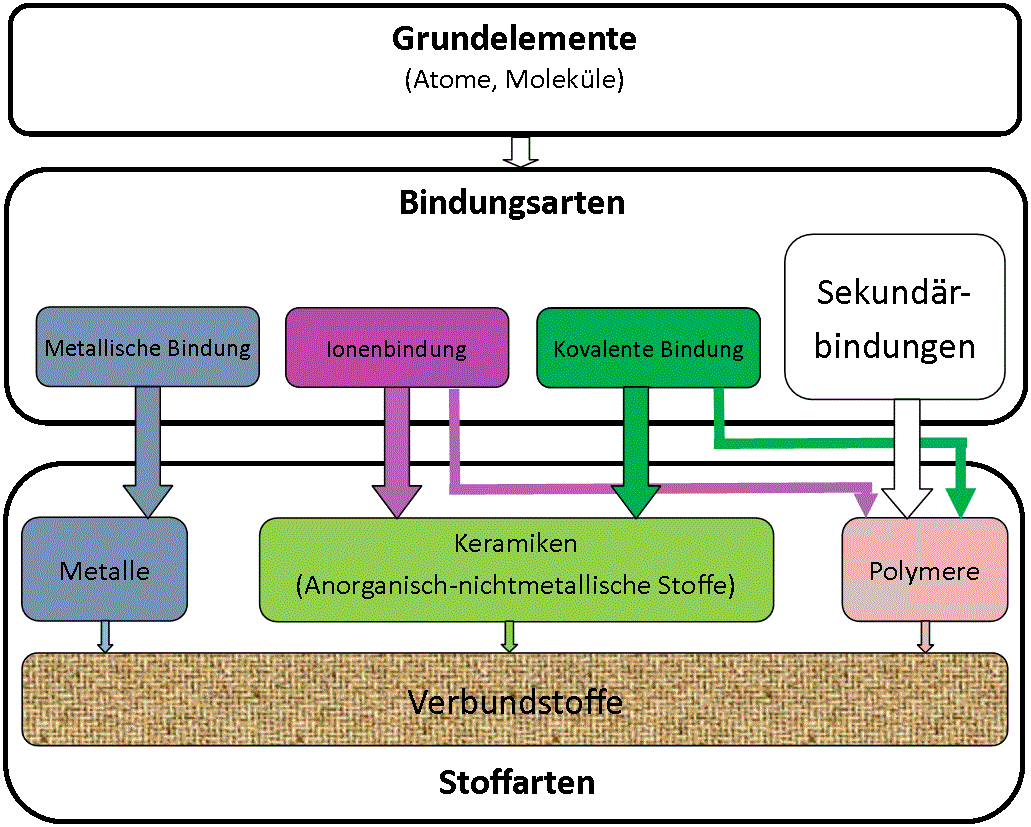
- Die metallische Bindung beruht auf dem Vorhandensein frei beweglicher Elektronen zwischen positiven Metallionen. Die frei beweglichen Elektronen kompensieren die abstoßenden Kräfte zwischen den Metallionen und halten diese auf ihren Plätzen. Die Plätze sind Gitterpunkte in unterschiedlichen Raumgittern. Die Gittertypen bestimmen sich aufgrund der Atomarten.
- Eine Ionenbindung tritt zwischen unterschiedlichen Atomarten dadurch auf, dass einige Atomarten leichter Elektronen abgeben, andere diese leichter aufnehmen. Das führt zu positiven Ionen der einen Art und negativen Ionen der anderen Art. Beide Arten ziehen sich gegenseitig elektrostatisch an. Dabei ordnen sie sich so an, dass die Ladung makroskopisch ausgeglichen ist. Aufgrund der Atomgrößen und Anzahl der an den Ladungen teilnehmenden Elektronen bilden sich Moleküle in passender Form oder Festkörper bestimmter Strukturen aus, wie zum Beispiel Raumgitter.
- Eine kovalente Bindung tritt dadurch auf, dass sich aus benachbarten Atomen Elektronenpaare bilden und somit zu stabilen Molekülen oder Festkörperkristallen führen. Rein kovalente Bindungen sind nur mit gleichen Elementen möglich. In Festkörpern sind dies die Elemente der vierten Hauptgruppe und das Bor. In anderen Stoffen wird der kovalente Bindungsanteil mit einem mehr oder weniger großen Ionenanteil überlagert.
Diese drei Bindungsarten sind primäre Bindungen, also Bindungen zwischen Atomen und weisen damit eine hohe Bindungsenergie auf.
- Die Sekundärbindung, eine weitere Bindungsart, beruht auf Anziehung in Dipolfeldern. Diese wirken zwischen polaren Bausteinen (Molekülen, Atomen) auch in größeren Abständen aber sind sehr viel schwächer als die Primärbindungen. Die polaren Bausteine sind aus Primärbindungen aufgebaut oder entstehen durch induzierte elektrostatische Ladungsverschiebung. Eine Gruppe der festen Polymere und auch der Flüssigkeiten erhalten ihre Struktur über diese Bindungsart.
Einige Aussagen zum Verhalten der Stoffe lassen sich direkt aus den Bindungsarten ableiten, Tabelle 1.
| Bindungsart | Eigenschaft der Bindung | Folge für den Stoff |
| Metallische Bindung | nicht gerichtet; Zusammenhalt der Rümpfe durch freie Elektronen (ohne Platzbindung); schwach bis stark (Bindungsenergie niedrig bis hoch, allgemein nicht hoch) | bleibend verformbar, da Platzwechsel der Atome elektrostatisch möglich; Siedetemperatur oder Schmelztemperatur niedrig bis hoch; chemisch meist nicht beständig; optisch reflektierend; elektrisch guter Leiter |
| Ionenbindung (heteropolare oder elektrovalente Bindung) | nicht gerichtet; weitreichend; makroskopisch elektrisch neutral; stark (hohe Bindungsenergie) | spröde, da Platzwechsel der Atome elektrostatisch schwer; hohe Härte; hohe Siedetemperatur oder Schmelztemperatur; optisch transparent; meistens Nichtleiter; chemisch meist beständig; unbeständig in polaren Lösungsmitteln |
| Atombindung (homöopolare, Elektronenpaar-, oder kovalente Bindung) | gerichtet (Platzwechsel nicht möglich); nur Nahwirkung; stark (hohe Bindungsenergie) | spröde, da gerichtete Bindung; hohe Siede- und Schmelztemperatur; hohe Härte; optisch transparent; meist Nichtleiter; chemisch beständig |
| Sekundärbindung | Dipolbindungen; halb gerichtet; weitreichend; sehr schwach (sehr niedrige Bindungsenergie) | chemisch beständig; niedrige Schmelztemperatur; geringe Härte; elektrisch isolierend; optisch transparent |
Neben diesen offensichtlichen, direkt aus dem Aufbau abgeleiteten Folgen für die Stoffe, sind zum Verständnis der Vorgänge bei deren Bearbeitung mit Laserstrahlen noch Kenntnisse zu weiteren Eigenschaften nötig und auch besondere physikalische Gesetzmäßigkeiten, die das Verhalten von Stoffen bei ihrer Bearbeitung mit Laserstrahlen erkennen lassen. Das Thema wird in den nächsten Kapiteln nach folgender Gliederung behandelt:
- Stoffeigenschaften
- Wärmeleitung
- Diffusion
- Phasenumwandlung
Nicht aufgegriffen werde hier besondere Eigenschaften, welche für Werkstoffe bedeutend sind:die fertigungstechnischen Eigenschaften, die Gebrauchseigenschaften sowie die wirtschaftlichen Eigenschaften Verfügbarkeit und Preis.
2 STOFFEIGENSCHAFTEN
Eigenschaften von Stoffen sind heute sehr umfangreich erfasst und auch naturwissenschaftlich beschrieben. Eine Ordnung entsprechend folgender Gliederung erleichtert das Einbeziehen dieser Stoffeigenschaften, um Randbedingen beim Arbeiten mit Laserstrahlen beurteilen zu können.
- Thermophysikalische Eigenschaften
- Chemische Eigenschaften
- Optische Eigenschaften
- Mechanische und technologische Eigenschaften
- Toxische Eigenschaften
2.1 THERMOPHYSIKALISCHE EIGENSCHAFTEN
Zu Beginn werden Definitionen der Größen zusammengefasst, die das Verständnis der weiteren Ausführungen erleichtern:
Thermodynamik
Die Thermodynamik ist ein Teilgebiet der Physik, das sich
mit Wärmeerscheinungen befasst, insbesondere mit der
Umwandlung der Energieform Wärme in eine andere oder
umgekehrt. Die klassische Thermodynamik untersucht
Gleichgewichtszustände makroskopischer Systeme sowie die
Zustandsänderungen beim Übergang von einem
Gleichgewichtszustand in einen anderen, die mit Zufuhr oder
Abfuhr von Wärme oder mechanischer Energie sowie
Temperaturänderungen verbunden sind.
Energie eines Systems
Energie bezeichnet das Arbeitsvermögen eines Systems. Sie
kann in verschiedenen Formen vorliegen. Ein System führt
äußere Energie in Form von kinetischer Energie Ekin,
oder potentieller Energie Epot mit sich
und innere Energien thermischer, chemischer,
elektromagnetischer oder mechanischer Art. Die äußere
(potentielle und kinetische) Energie wird im Folgenden nicht
betrachtet. Von der im System vorhandenen Energie wird je
nach Eigenart der Umwandlungsmöglichkeiten die Energie
allgemein, die innere Energie, die Wärme, die Enthalpie, die
freie Energie und die freie Enthalpie betrachtet.
Zustand
Der Zustand eines thermodynamischen Systems wird durch einen
Satz von thermodynamischen Zustandsgrößen festgelegt:
Temperatur, Druck, Volumen, Energie, Entropie, Enthalpie und
andere. Diese beschreiben den Zustand – unabhängig davon,
wie dieser erreicht wurde. Sie lassen sich einteilen in
intensive und extensive Zustandsgrößen. Intensive
Zustandsgrößen sind unabhängig von der Größe des Systems,
wie beispielsweise Temperatur oder Druck. Extensive
Zustandsgrößen ändern sich gleichsinnig mit der Größe des
Systems wie Stoffmenge oder Entropie.
Temperatur
Die Temperatur T ist eine intensive Zustandsgröße,
die den Wärmezustand eines Stoffes beschreibt. Sie ist ein
Maß für die mittlere kinetische Energie der
Mikrostruktur-Bausteine (Atome, Moleküle) eines Systems.
Wärme
Die Wärme Q ist eine Energieform, die aufgrund eines
Temperaturgefälles ΔT zwischen Systemen und Umgebung übertragen wird:
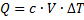 ,
oder
,
oder
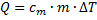
mit der Wärmekapazitätsdichte c oder der spezifischen Wärmekapazität cm, dem Volumen V, der Masse m.
Innere Energie
Die innere Energie U(S, V, ni) ist
die Energie, die als Wärme Q und Arbeit W
mit der Umgebung ausgetauscht wird. Sie ist daher eine
extensive Zustandsgröße und Messungen nur über Änderung ΔU
des Zustandes zugänglich.
ΔU = U2 – U1 = ΔQ + ΔW
Arbeit
Die Arbeit Wist eine Energieform, die mechanisch
oder elektromagnetisch übertragen wird.
Enthalpie
Die Enthalpie H ist eine extensive thermodynamische
Zustandsgröße eines Systems als Summe der inneren Energie U und der Volumenarbeit.
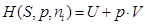
|
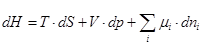
|
Freie Energie (Helmholtz-Funktion)
Die freie Energie F ist eine extensive
thermodynamische Zustandsgröße. Sie beinhaltet denjenigen
Teil der inneren Energie U eines Systems, der bei
einem umkehrbaren isothermen Prozess als Arbeit nach außen
abgegeben werden kann.
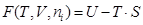 |
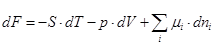 |
Freie Enthalpie (Gibbssche Freie Enthalpie)
Die freie Enthalpie G ist der Teil der Enthalpie,
der bei umkehrbaren isobaren Prozessführungen in jede
beliebige Energieform umwandelbar ist.
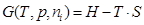 |
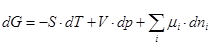 |
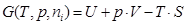 |
Entropie
Die Entropie S ist ein Maß für den Ordnungszustand
thermodynamischer Systeme. Sie ist eine extensive
Zustandsgröße. Definiert wird sie über das Differential dS = dQ / T.
Bei Vorgängen in abgeschlossenen Systemen ist S
dann konstant, wenn diese umkehrbar sind, das heißt, dS = 0.
Für nicht umkehrbare Vorgänge gilt dS > 0, das
heißt, die Entropie eines abgeschlossenen Systems kann nicht
abnehmen.
Chemisches Potential
Das chemische Potential µB einer
Komponente B einer Mischphase ist die partielle
molare freie Enthalpie in der Mischphase
Thermophysikalische Eigenschaften der Stoffe – also physikalische Eigenschaften, die mit deren Temperatur in Beziehung stehen – sind die wesentlichen Stoffeigenschaften in den überwiegenden Fällen der Bearbeitung mit dem Laserstrahl. Bei allen Bearbeitungen von Materialien wirkt der Laserstrahl auch thermisch. Im Vordergrund stehen die energetischen Eigenschaften; denn der Laserstrahl überträgt Leistung in den Stoff und ändert damit dessen Energieinhalt. Von Interesse sind daher die Stoffdaten („Stoffkonstanten“) Wärmekapazitätsdichte c, welche das Energiespeichervermögen beschreibt, und die Wärmeleitfähigkeit λ, welche den Leistungsfluss bestimmt. Diese hängen deutlich von der Temperatur und weiteren Zustandsgrößen ab und sollten daher in Betrachtungen zur Materialbearbeitung mit Laserstrahlen nicht als echte Konstanten einbezogen werden.
In der Wärmekapazitätsdichte c wird die
Wärmekapazität auf das Volumen bezogen und nicht auf die
Masse wie in der spezifischen Wärmekapazität, die in
Tabellenwerken für sehr viele Stoffe und weite
Temperaturbereiche zu finden ist; denn die
Bearbeitungsverfahren werden primär auf Geometrien
abgestimmt und nicht auf Massen oder Stoffmengen. Falls hier
Massenbezug diskutiert wird, dann ist c mit dem
Index m gekennzeichnet. Die beiden Größen zum
Energiespeichervermögen c und cm
sind über die Dichte ρ des Stoffes verbunden
mit der (massenbezogenen) spezifischen Wärmekapazität cm
und der Dichte ρ:
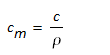
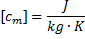
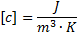
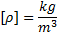
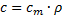
Zum Energiespeichervermögen tragen Übergänge zwischen Modifikationen von Stoffzuständen bei, zum Beispiel Übergänge zwischen verschiedenen Phasen eines Stoffes wie flüssig – fest, ferromagnetisch – diamagnetisch, austenitische Gitter – ferritische Gitter. Daneben sind Bildungsenergien, Aktivierungsenergien, Grenzflächenenergien und andere zu beachten. Einzelheiten dazu sind in den verschiedenen Lehrbüchern zur Werkstoffkunde behandelt. Ein grundlegendes Werk von Kubaschewski et al. gibt Messergebnisse der Thermophysikalischen Daten vieler Stoffe mit deren Temperaturabhängigkeiten wieder und liefert auch die theoretischen Grundlagen. [2]
Als Hilfe für Berechnungen zu den thermischen Verfahren in der Materialbearbeitung mit Laserstrahlen, wie Schweißen, Schneiden, Abtragen und für die Randschichtearbeitung, sind im Folgenden ausgewählte Stoffdaten in Tabellenform zusammengestellt, Tabelle 2. Da die Berechnungen sich auf ingenieurwissen-schaftliche Betrachtungen beziehen, wird auch hier konsequent ein Volumenbezug der Größen in den Vordergrund gestell und nicht, wie bei Physikern üblich, ein Bezug auf die Masse.
| Stoff | M | N | ρk | ρf | Tkf | Tfd | ΔHfest | ΔHkf | ΔHf | ΔHfd | HS | HD |
| Ein heit |
g/mol | 1022/ cm³ | g/cm³ | K | K | K | J/mm³ | kJ/mol | kJ/mol | kJ/mol | J/mm³ | J/mm³ |
| C | 12 | 3,51 | 4098 | 4098 | 105,00 | 715,00 | 30,68 | 239,6 | ||||
| Mg | 24 | 4,30 | 1,74 | 1,57 | 922 | 1380 | 1,27 | 8,95 | 14,80 | 131,90 | 1,91 | 12,41 |
| Al | 27 | 6,02 | 2,70 | 2,37 | 933 | 2793 | 1,72 | 10,70 | 52,40 | 284,10 | 2,79 | 36,44 |
| Si | 28 | 4,98 | 2,33 | 2,53 | 1685 | 3514 | 3,00 | 50,30 | 136,00 | 385,60 | 7,18 | 50,59 |
| Ti | 48 | 6,68 | 4,51 | 4,20 | 1943 | 3562 | 5,09 | 19,30 | 52,90 | 422,90 | 6,91 | 51,72 |
| Cr | 64 | 8,48 | 8,96 | 8,00 | 1358 | 2836 | 4,16 | 13,00 | 46,40 | 304,80 | 6,00 | 55,55 |
| Mn | 55 | 7,47 | 1517 | 2235 | 6,42 | 12,05 | 33,07 | 226,00 | 8,06 | 43,28 | ||
| Fe | 56 | 8,48 | 7,87 | 7,00 | 1809 | 3135 | 9,17 | 19,40 | 55,50 | 353,80 | 11,90 | 69,63 |
| Ni | 59 | 9,13 | 8,91 | 7,80 | 1726 | 3187 | 7,19 | 17,20 | 56,30 | 378,80 | 9,81 | 75,85 |
| Co | 59 | 8,99 | 8,89 | 7,70 | 1768 | 3201 | 8,15 | 16,19 | 49,80 | 373,30 | 10,59 | 74,45 |
| Cu | 64 | 8,48 | 8,96 | 8,00 | 1358 | 2836 | 4,16 | 13,00 | 46,40 | 304,80 | 6,00 | 55,55 |
| Zn | 65 | 6,55 | 7,14 | 6,66 | 693 | 1180 | 1,18 | 6,70 | 15,30 | 114,80 | 1,91 | 16,11 |
| Ge | 73 | 4,43 | 5,32 | 5,50 | 1211 | 3093 | 1,89 | 36,94 | 58,00 | 330,90 | 4,60 | 33,10 |
| Zr | 91 | 6,51 | 2128 | 4682 | 4,51 | 16,20 | 45,00 | 590,50 | 5,67 | 51,02 | ||
| Mo | 96 | 10,28 | 2890 | 4912 | 9,27 | 39,00 | 81,49 | 598,00 | 13,44 | 86,25 | ||
| Pd | 106 | 6,77 | 12,02 | 10,70 | 1825 | 3237 | 5,24 | 16,74 | 53,20 | 372,60 | 7,13 | 55,24 |
| Ag | 108 | 5,85 | 10,49 | 9,30 | 1235 | 24,85 | 2,27 | 11,30 | 37,20 | 250,60 | 3,36 | 31,34 |
| Cd | 112 | 4,60 | 8,60 | 8,00 | 594 | 1040 | 0,63 | 6,10 | 13,30 | 99,40 | 1,09 | 9,72 |
| Sn | 119 | 3,70 | 7,29 | 6,96 | 505 | 2876 | 0,36 | 7,20 | 72,50 | 230,20 | 0,80 | 19,39 |
| Sb | 122 | 3,27 | 6,69 | 6,50 | 904 | 1860 | 0,91 | 19,83 | 30,10 | 195,50 | 2,00 | 14,39 |
| Ta | 181 | 5,35 | 16,60 | 15,00 | 3287 | 5731 | 8,75 | 31,50 | 95,50 | 735,40 | 11,64 | 87,88 |
| W | 184 | 6,32 | 19,30 | 17,70 | 3680 | 5828 | 10,77 | 35,30 | 77,20 | 774,60 | 14,47 | 103,87 |
| Pt | 195 | 6,26 | 21,45 | 18,90 | 2045 | 4100 | 8,88 | 19,66 | 77,50 | 510,45 | 8,04 | 72,68 |
| Au | 197 | 5,91 | 19,32 | 17,30 | 1338 | 3130 | 2,86 | 12,36 | 52,60 | 324,43 | 4,08 | 41,05 |
| Pb | 207 | 3,29 | 11,34 | 10,60 | 601 | 2023 | 0,47 | 4,77 | 40,40 | 177,90 | 0,73 | 12,67 |
Bemerkenswertes zeigt die letzte Spalte unter HD an. HD ist die Wärme, die von Raumtemperatur bis hinein in den Dampfzustand aufgebracht wird. Diese ist im Kohlenstoff die höchste, gefolgt von der in Wofram.
Betont wird hier, dass sich die Wärmeinhalte auf die Volumina beziehen; denn diese beinhalten Abmessungen, welche für die Bearbeitung von Stoffen – insbesondere von Werkstoffen – ausschlaggebend sind. Die Wärme im Dampf bestimmt energetisch die Prozesse "Tiefschweißen", "Sublimierschneiden" und einige Abtragverfahren.
2.2 Chemische Eigenschaften
Die Chemie befasst sich mit dem Aufbau, den Eigenschaften und der Umwandlung von Stoffen. Im Vordergrund stehen hierbei Kenntnisse über die Elektronenhüllen der Stoffbausteine. Diese bestimmen die chemischen Eigenschaften.
Chemische Eigenschaften der Stoffe lassen sich für die Bearbeitung von Stoffen mit Laserstrahlen in den Stoffen selbst und in Reaktionen mit anderen Stoffen nutzen. Dies kann sowohl indirekt über das gezielte Einbringen thermischer Energie oder direkt über das Einbringen von Photonenenergie in Atome oder Moleküle erfolgen. So beruht das Laserstrahl-Brennschneiden auf dem Erwärmen durch den Laserstrahl wodurch die Oxidation von Metallen im Schneidstrahl aus Sauerstoff oder anderen Gasen beschleunigt wird. Dies ist ein Beispiel für gezieltes Einbringen von Wärmeenergie, um zwei Stoffe reagieren zu lassen.
Als Beispiel für eine Direkte Wirkung von Photonen auf einen Stoff sei hier das aus der Fotographie bekannte Trennen von Silberhalogeniden wie AgCl genannt. Hier genügt die geringe Photonenernergie von Licht.
Der Hinweis auf die Möglichkeiten soll hier genügen.
2.3 Optische Eigenschaften
Die optischen Eigenschaften eines Stoffes beschränken sich auf vier physikalische Größen im Verhalten gegenüber Strahlung.
- Absorption
- Reflexion
- Transmission
- Streuung
Die Strahlung ist mit einem Leistungsfluss verbunden, so dass diese vier optischen Eigenschaften energetische Eigenschaften sind, die nur im Zusammenhang mit der Strahlung selbst definiert sind. Daher werden diese optischen Eigenschaften im Kapitel Wechselwirkung behandelt.
Strahlung, so auch die optische Strahlung, die auf einen Stoff trifft, kann von diesem absorbiert werden, (Absorption), reflektiert (Reflexion), hindurchgelassen (Transmission), oder gesteut werden. Die Absorption kann in der Randschicht des Stoffes oder (bei Transmission) im Inneren erfolgen. Streuung ist sowohl in der Randschicht als auch im Inneren der Stoffe möglich. Das Gesetz zur Energieerhaltung sagt zudem, das die vier Möglichkeiten zusammen das Verhalten des gesamten Anteil der auftreffenden Strahlungsleistung umfassen. Die Summe der vier Leistungsanteile ist gleich der einfallenden Leistung.
2.4 Mechanische und technologische Eigenschaften
Zunächst ein paar Worte zum Begriff "technolgische Eigenschaften". Dieser beinhaltet mehr als "mechanische Eigenschaften", auch wenn diese Eigenschaften nach mechanischer oder chemischer Beanspruchung sichtbar werden. Als Beispiel soll hier der Übergang von der Hochlage in den Sprödbruch in Kerbschlag-Biegeversuchen genannt werden. Von Werkstoffen insbesondere fallen Verarbeitungseigenschaften wie Schweißbarkeit und Härtbarkeit darunter und auch das Gebrauchsverhalten unter bestimmten betriebsnahen Beanspruchungen.
Eine zentrale Rolle im Feld der mechanischen Eigenschaften spielt die Festigkeit. Festigkeit kann unterschiedlich sein als Eigenschaft eines Werkstoffs Bauteils aus diesem Werkstoff. Allein der Begriff "Festigkeit" auf den Werkstoff bezogen umfasst mehrere Aspekte, die eine nährere Beschreibung fordern. Heute wird eine Unterteilung in drei Klassen gewählt, die auf gänzlich unterschiedliche Eigenschaften des Mikrostrukturaufbaus der Stoffe zurückgeführt werden können:
- Widerstand gegen bleibende Formänderungen
- Widerstand gegen Ausbreitung von Rissen
- Widerstand gegen das Abtragen von Randschichten (Oberflächen)
Daraus wird eine Vielfalt von Eigenschaftsänderungen ersichtlich, die gewollt oder ungewollt bei thermischer Bearbeitung von Stoffen mit Laserstrahlen auftreten können. Insbesondere ein Erhöhen des Widerstandes gegen bleibende Formänderung verringert häufig den Widerstand gegen das Aubreiten von Rissen.
Die hier aufgezeigten Aspekte der mechanischen und technolgischen Eigenschaften deuten die Komplexität des Gebietes an.
Die Überschrift "Mechanische und technologische Eigenschaften" wurde hier eingebracht, um auf die in den Referenzen aufgeführen Lehrbücher zu verweisen. Das Gebiet ist derart weit gespannt, dass hier weitere Ausführungen nicht helfen würden, die Grundlagen zur Materialbearbeitung mit Laserstrahlen als relativ neue Technik zu erfassen.
2.5 Toxische Eigenschaften
Auf toxische Eigenschaften sei hier nur verwiesen, da diese in den Sicherheitsrichtlinien für die Bearbeitung der Stoffe aufgeführt sind. Zusätzlich allerdings sollte daran gedacht werden, dass bei den möglichen hohen Leistungsdichten in Laseratrahlen jeder Stoff verdampft oder zersetzt werden kann. Als Beispiel sei hier der toxisch unkritische Stoff "Gips" genannt, dessen Zersetzugsprodukte eben auch Schwefelsäuretropfen enthalten. Zusätzlich können chemische Reaktionen aufgrund temperaturbedingter hochenergetischer UV-Strahlung eines sekundären Plasmas auch unproblematisch erscheinende Stoffe in toxische Verbindungen überführen.
3 WÄRMELEITUNG
Wenn Wärme in einen Stoffbereich eingebracht wird, dann strömt diese in die Umgebung mit geringerer Temperatur, in dem Bestreben, die Temperatur auszugleichen. Der Wärmefluss ist ein Energietransport ohne Stoffstrom zwischen unterschiedlichen Temperaturniveaus im Stoff. Er wird durch den Temperaturunterschied sowie durch Eigenschaften des Stoffes bestimmt. Die Größen der Stoffeigenschaften sind Wärmeleitfähigkeit λ und auch Wärmekapazitätsdichte c der Stoffe. Ein Transport von Wärmeenergie Q aus einem Bereich in einen anderen bedeutet, dass eine Leistung P fließt.
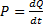
Aus dem Leistungsfluss andererseits ergibt sich die eingebrachte Wärmemenge Q zu
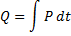
Wird der Leistungsfluss auf eine Fläche der Größe 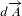 bezogen,
dann definiert sich die Wärmestromdichte
bezogen,
dann definiert sich die Wärmestromdichte 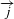 mit
mit 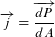
Die Wärmestromdichte wird über die Wärmeleitungsgleichung
berechenbar. In homogenen isotropen [3] Medien lautet diese
für den stationären Fall, das heißt der Temperaturgradient 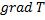 ist
zeitlich konstant:
ist
zeitlich konstant:
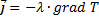 .
.
Hieraus ergibt sich der Leistungstransport:
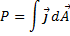
und im einfachen Fall der linearen (ebenen) Wärmeleitung in
x-Richtung – dieser reicht für viele Abschätzungen in
der Materialbearbeitung mit Laserstrahlen aus:
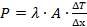 (1)
(1)
wobei A die von der Wärme durchströmte ebene Querschnittsfläche und ΔT der Temperaturunterschied im Abstand Δx ist.
Eine wesentliche Rolle für Betrachtungen in der Materialbearbeitung spielt die Zeitabhängigkeit; denn ein Vorteil des Einsatzes von Laserstrahlen liegt in möglichen kurzen Bearbeitungszeiten. In diesem Fall wird die allgemeine Wärmeleitungsgleichung hinzugezogen.
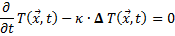
wobei ![]() die Temperatur an der Stelle
die Temperatur an der Stelle
![]() zum Zeitpunkt t, Δ
der Laplace-Operator und die Konstante
zum Zeitpunkt t, Δ
der Laplace-Operator und die Konstante 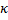 die Temperaturleitfähigkeit
des Mediums ist.
die Temperaturleitfähigkeit
des Mediums ist.
Eine für die weiteren Betrachtungen ausreichende Vereinfachung berücksichtigt nur eine Raumdimension der linearen (ebenen) Wärmeleitung und beschreibt die zeitliche Änderung der Temperatur in einer Dimension, hier in x-Richtung. Dadurch wird der Laplace-Operator zu einer einfachen zweiten Ableitung:
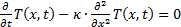 (2)
(2)
Hierin ist κ die Temperaturleitfähigkeit oder
Wärmediffusionskonstante. Diese ist über die
Wärmekapazitätsdichte c des Stoffes mit dessen
Wärmeleitfähigkeit 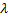 verbunden über
verbunden über
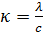 (3)
(3)
Oder, wenn die spezifische Wärmekapazität verwendet wird
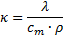
Aus der allgemeinen Wärmeleitungsgleichung lässt sich eine
für die Ausbreitung von Wärme in Stoffen weitere hilfreiche
Größe ableiten: die Relaxationszeit  .
.
Die allgemeine Wärmeleitungsgleichung führt nur in
Spezialfällen zu analytischen Lösungen. Heute werden deshalb
Finite-Elemente-Programme verwendet. Für den linearen Fall
(eindimensionale ebene Wärmeleitung) lassen sich Lösungen
analytisch ermitteln, beispielsweise für einen
halbunendlichen Körper (ein unendlich ausgedehnter Körper,
der auf einer Seite durch eine Ebene begrenzt ist) mit einer
Ausgangstemperatur T2 und ab einem
Zeitpunkt t = 0 in der Begrenzungsebene eine
Ebenentemperatur T1. Diese wird konstant
gehalten und dehnt sich dann ins Stoffinnere aus, Gleichung
(4), Bild 2.
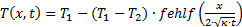 (4)
(4)
In der Beispielsrechnung wird die Stofftemperatur mit T2
= 20 °C angesetzt, die Starttemperatur T1
an der Oberfläche zur Zeit t = 0 mit
800 °C.
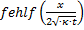 ist die Gaußsche Fehlerfunktion, angewandt auf die Koordinate x
zur Zeit t mit der Diffusionskonstanten κ.
ist die Gaußsche Fehlerfunktion, angewandt auf die Koordinate x
zur Zeit t mit der Diffusionskonstanten κ.
Der Term 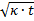 hat eine
besondere Bedeutung. Seine Dimension ist die einer Länge. Er
definiert eine Relaxationslänge in der Wärmeausbreitung, so
wie sie für Abschätzungen von Ergebnissen in der
Materialbearbeitung besonders hilfreich ist. Am Ort
hat eine
besondere Bedeutung. Seine Dimension ist die einer Länge. Er
definiert eine Relaxationslänge in der Wärmeausbreitung, so
wie sie für Abschätzungen von Ergebnissen in der
Materialbearbeitung besonders hilfreich ist. Am Ort 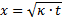 ist nach
Gleichung (4) die Körpertemperatur um etwa die Hälfte der
Temperaturdifferenz angestiegen. Der genaue Wert ist
ist nach
Gleichung (4) die Körpertemperatur um etwa die Hälfte der
Temperaturdifferenz angestiegen. Der genaue Wert ist 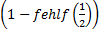 . Die Zeit
für diesen Relaxationsweg wird als Relaxationszeit
. Die Zeit
für diesen Relaxationsweg wird als Relaxationszeit  definiert,
Gleichung (5).
definiert,
Gleichung (5).
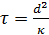 (5)
(5)
In der Materialbearbeitung werden häufig Temperaturverhältnisse von etwa 1/2 betrachtet, wie Schmelztemperatur zur Siedetemperatur; Härtetemperatur zur Schmelztemperatur; oder Austenit-Temperatur zur Martensit-Temperatur. Somit ist die einfach einzuprägende Relaxationsgleichung besonders hilfreich; denn diese bezieht sich auf etwa die halbe Temperaturdifferenz.
Die Relaxationsgleichung, Gleichung (5), zeigt einen
quadratischen Zusammenhang zwischen Eindringtiefe und
Zeitaufwand. Das Eindringen einer Temperaturfront in die
doppelte Tiefe d erfordert daher die
vierfache Zeit
t, Bild 2.
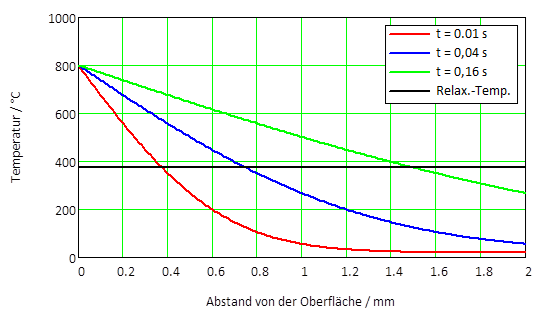
Zum Zeitpunkt t = 0 wird die Oberfläche eines halbunendlichen Körpers aus Stahl mit der Temperatur T2 = 20 °C auf die Temperatur T1 = 800 °C erwärmt. Diese Temperatur wird gehalten. Die Erwärmung breitet sich in die Tiefe aus. Der Temperaturverlauf für die Zeiten 10 ms, 40 ms und 160 ms ist eingetragen, dazu die Relaxationstemperatur.
Der Berechnung liegt die Wärmediffusionskonstante κ = 12,5 mm² / s zugrunde. Das entspricht der von Baustahl bei 400 °C. Die Wärmediffusionskonstanten hängen allerdings von der Temperatur ab. Für eine Abschätzung ist diese Abhängigkeit jedoch vernachlässigbar.
3.1 Zusammenstellung von Gleichungen zur Wärmeleitung
Die folgende Zusammenstellung dient dem Ziel, die für Berechnungen von Ergebnissen in der industriellen Materialbearbeitung mit Laserstrahlen hilfreichen Gleichungen in einer Übersicht parat zu haben. Damit wird das zeitraubende Aufsuchen von Fachliteratur und dem anschließenden Auswählen der Gesetze, die gerade von Interesse sind, abgekürzt. Ein Hinweis: Die gleichen Formalismen, die dem Verständnis des Wärmestroms dienen, gelten auch für den Stoffstrom, siehe 4. Diffusion.
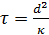 |
Eingetragen Wärmeenergie aus der Leistung P(t) in der Zeit von t1 bis t2 |
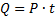 |
Eingetragene Wärmeenergie bei konstanter Leistung |
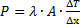 |
Stationäre Wärmeleitungsgleichung für den eindimensionalen ebenen Fall |
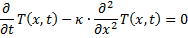 |
Instationäre Wärmeleitungsgleichung für den eindimensionalen ebenen Fall |
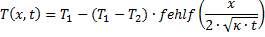 |
Spezielle Lösung der Instationären Wärmeleitungsgleichung für den ebenen Fall |
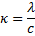 |
Wärmediffusionskonstante |
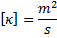 |
Dimension der Wärmediffusionskonstanten |
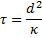 |
Relaxationszeit für die Eindringtiefe d einer Temperaturfront zum Ausgleich auf etwa die halbe Temperaturdifferenz |
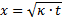 |
Eindringtiefe x einer Temperaturfront in der Zeit t zum Ausgleich auf etwa die halbe Temperaturdifferenz |
4 DIFFUSION
Diffusion ist ein Stofftransport durch thermische
Aktivierung. Innerhalb von Festkörpern ist sie auch die
einzige Möglichkeit des Stofftransports. Ermöglicht wird
dieser über ungeordnete temperaturbedingte Schwingungen der
Mikrostruktur-Bausteine (Atome, Moleküle) um deren Ruhelage.
Die Temperatur ist eine intensive Zustandsgröße und
kennzeichnet den Schwingungszustand der
Mikrostruktur-Bausteine. Sie ist ein Maß für deren mittlere
kinetische Energie. Die Schwingungsamplitude der Bausteine
steigt mit der Temperatur. Bei Schmelztemperatur von
kristallinen Stoffen mit Primärbindungen zum Beispiel
beträgt sie etwa 12 % des Gitterabstandes. Für technische
Anwendungen setzt Diffusion bei etwa 30 % der
Schmelztemperatur
merkbar ein. [4],
Diffusionsarten:
- • Zwischengitterdiffusion
(interstitielle Diffusion) - • substituierende Diffusion
Der Begriff „Zwischengitterdiffusion“ gilt strenggenommen nur für Kristalle oder kristalline Stoffe, wird aber auch für amorphe verwendet. Besser wäre die Verwendung Zwischenraum-Diffusion; diese entspricht dem lateinisierten Begriff.
Eine substituierende Diffusion in kristallinen Festkörpern erfolgt praktisch nur über Baufehler der Kristallite wie Leerstellen, Bild 3. In diesem Kugelmodell sind einige Positionen mit roten Kugeln besetzt. Die stellen Fremdatome dar. Die Kugeln sind elastisch.
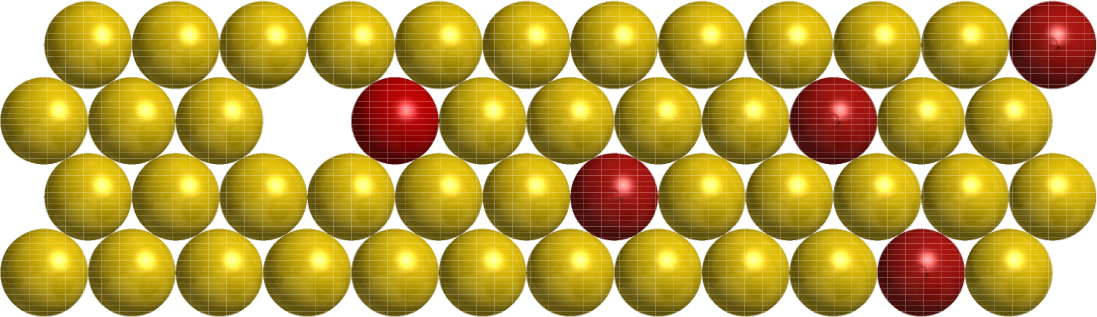
In der Anordnung der gelben Kugeln fehlt ein Element. Das ist die Leerstelle. Einige andere Positionen sind durch fremde rote ersetzt. Nach rechts nimmt die Anzahl der roten Kugeln zu. Damit wird ein Konzentrationsgradient angedeutet.
Die Leerstelle kann durch direkt benachbarte Kugeln besetzt werden, wenn sie eine Barriere elastischer Energie, die Verengung des Wegs durch andere Kugeln, überwinden. Die Energie wird thermisch eingebracht. Die Leerstelle nimmt die frei gewordene Position ein. Alle Wege der direkten Nachbarn in die Leerstelle sind gleich wahrscheinlich. Also wird sich die Leerstelle ohne Vorzugsrichtung irgendwie im Raum bewegen. Makroskopisch wird kein Stoff transportiert.
Für Diffusion mit makroskopischem Stofftransport muss eine „treibende Größe“ vorhanden sein. Das sind Konzentrations- oder Temperaturgefälle oder örtliche Unterschiede anderer Größen, welche zum Energieinhalt des Stoffes beitragen. Diese örtlichen Unterschiede werden mit dem Begriff „Gradient“ physikalisch erfasst. Im Modell Bild 3 sind rechts mehr Fremdatome (der Konzentrations-Gradient ist nach rechts positiv). Daher ist die Wahrscheinlichkeit größer, dass ein Fremdatom von rechts die Leerstelle links besetzt. Also werden mehr Fremdatome entgegen dem Gradienten transportiert als in seine Richtung. Damit findet makroskopischer Stofftransport statt.
Bei einer interstitiellen Diffusion bewegen sich Mikrostruktur-Bausteine zwischen den Elementen hindurch, die den Stoffaufbau bestimmen. Dies ist für kleine Elemente leichter als für große. Die diffundierenden Elemente werden ähnlich wie in der Substitutions-Diffusion für jeden Platzwechsel Barrieren elastischer Energie überwinden.
Der makroskopische Teilchentransport lässt sich berechnen. Für den Fall, dass alle Größen, außer der betrachteten, konstant bleiben, erfolgt der makroskopische zeitliche Teilchentransport dn / dt durch eine Fläche A hindurch nach dem ersten Diffusionsgesetz (1. Ficksches Gesetz), das hier für den Fall eines räumlichen Konzentrations-Unterschiedes – also eines Konzentrationsgradienten – beschrieben wird:
1. Diffusionsgesetz:
Der Fluss von Mikrostruktur-Bausteinen in einem Stoff, das heißt die zeitliche Änderung der Teilchen-Anzahl dn/dt, ist proportional zur Fläche A, durch die der Stofftransport erfolgt, und einem Diffusionskoeffizienten D, Gleichung (6).
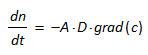 (6)
(6)
| n | Teilchen-Anzahl | [n] = 1 |
| A | Diffusionsfläche (Querschnittsfläche) | [A] = m2 |
| D | Diffusionskoeffizient (Diffusionskonstante) | [D] = m2 / s |
| c | Konzentration | [c] = 1 / m3 |
| t | Zeit | [t] = s |
Dieses Diffusionsgesetz beschreibt den stationären Fall. Zeitlich und räumlich ändert sich keine Größe. Das Minuszeichen bedeutet, dass der Stofftransport entgegen dem Konzentrations-Gradienten gerichtet ist. Der Diffusionskoeffizient D ist für jeden diffundierenden Stoff in den verschiedenen Grundstoffen jeweils eine andere Konstante. Diese ist zudem Temperatur- und Konzentrationsabhängig. Für weitere Abschätzung von Aussagen für die Materialbearbeitung mit Laserstrahlen reicht die Betrachtung der Temperaturabhängigkeit. Diese Abhängigkeit wird durch die Boltzmannverteilung von Zuständen bestimmt. Sie lässt sich berechnen, wenn die Aktivierungsenergie Hw für ein Mol von Platzwechseln bekannt ist (im Kugelmodell Bild 3 die elastische Schwellen-Energie). [5]
Aus der Boltzmann-Statistik wird Anzahl der Teilchen für ein Energieniveau ermittelt:
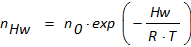 (7)
(7)
mit
| nHw | Teilchen-Anzahl der Energie Hw |
| n0 | Gesamt-Anzahl der Teilchen |
| HW | Aktivierungsenergie für Platzwechsel |
| R | universelle Gaskonstante |
| T | Temperatur |
Der Ansatz ergibt für die Diffusionskonstante D:
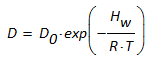 (8)
(8)
Falls Leerstellen für die Diffusion nötig sind:
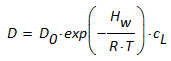 cL
Leerstellenkonzentration
cL
Leerstellenkonzentration
Die Leerstellenkonzentration cL ist ebenfalls temperaturabhängig nach der Boltzmannverteilung, daher führt diese Gleichung zu
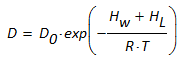
HL Aktivierungsenergie für Leerstellen
(9)
Gelegentlich werden die spezifischen Energien Hw und HL zusammengefasst zu Hw + HL = Q. Zur Erinnerung: R⋅T ist die thermische Energie pro Mol, kB⋅T die thermische Energie pro Atom.
Zu bemerken ist hier noch, dass diese Diffusionsgleichung für das thermodynamische Gleichgewicht gilt. Die Leerstellenkonzentration, und damit D, kann über Bestrahlung, Kaltverformung oder schnelles Abkühlen von hohen Temperaturen stark erhöht werden.
Einen weiteren Einfluss auf den makroskopischen Stofftransport, hat der Temperaturgradient. Dieser kann gerade für Betrachtungen in der Materialbearbeitung mit Laserstrahlen interessant sein; denn mit Hilfe von Laserstrahlen lassen sich auch räumlich eng begrenzte Bereiche mit hohen Temperaturgradienten in verschiedenste Stoffe einbringen.
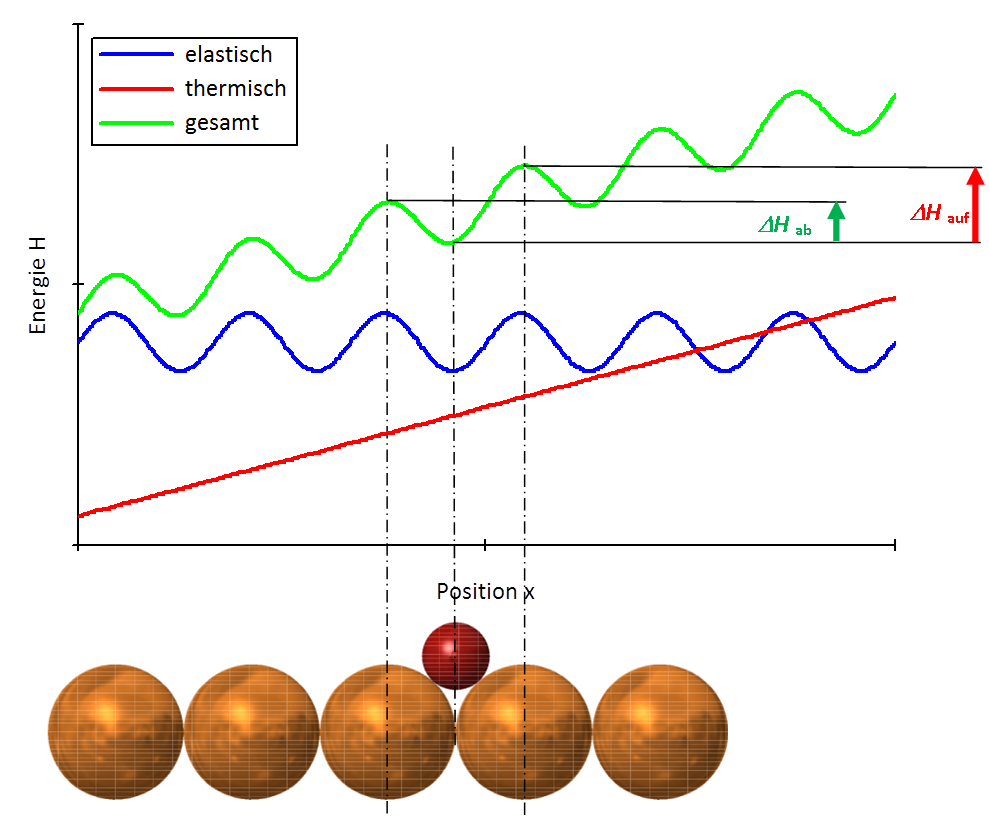
Das Fremdatom (kleine Kugel) durchläuft während des Wanderns entlang einer Atomreihe Minima und Maxima eines elastischen Potentials (blau). Wird ein Temperatur-Gradient eingebracht, addiert sich zu dem Potentialverlauf der Ebene der thermische Energieanteil (rot). Die Summe (grün) führt zum Erhöhen der Potentialschwelle in Gradienten-Richtung, zur Erniedrigung in entgegengesetzter Richtung.
Über diese wäre dann eine gerichtete Diffusion für Mikrostrukturierungen möglich. Auch in makroskopischer thermischer Bearbeitungen (Randschichtbearbeiten, Schweißen, Trennen) mit dem Werkzeug Laserstrahl können hohe Temperatur-gradienten auftreten, deren Auswirkung berücksichtigt werden sollte. Wegen der Komplexität der Grundlagen zu Gesetzen der allgemeinen Diffusion, wird hier lediglich der physikalische Hintergrund für die Auswirkung eines Temperaturgradienten aufgezeigt.
In einem Temperatur-Gradienten, das heißt in einem Gradienten thermischer Energie, setzt sich die ortsabhängige Gesamtenergie aus dem (periodischen) Anteil des Gitters und dem termischen Anteil des Temperatur-gradienten zusammen. Dadurch wird zum Überwinden der periodischen Schwelle in Gradienten-Richtung ΔHauf höher – entgegengesetzt ΔHab niedriger, Bild 4. So überwiegt ein Stofftransport in eine Richtung. Die Fremdatome diffundieren daher bevorzugt in Richtung der kühleren Seite.
Im eindimensionalen Fall, das heißt für eine ebene
Grenzfläche (hier senkrecht zur x-Richtung) ergibt sich
das 2. Diffusions-gesetz durch partielle Differentiation des 1.
Diffusionsgesetzes nach der Ortsvariablen x. Damit werden
örtliche und zeitliche Konzen-trationsunterschiede verknüpft.
Das gilt für den Fall konstanter Temperatur (zeitlich und
räumlich) dann, wenn keine weiteren treibenden Größen
beachtet werden müssen.
2. Diffusionsgesetz:
Das 2. Diffusionsgesetz wird üblicherweise als Differentialgleichung formuliert:
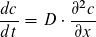 (10)
(10)
Eine Lösung der zweiten Diffusionsgleichung für den ebenen Fall ist
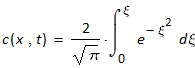 (11)
(11)
mit
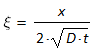 (12)
(12)
Der Ausdruck ist unter der Bezeichnung “Gaußsches Fehlerintegral” oder “Fehlerfunktion” bekannt.
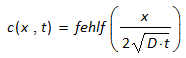 (13)
(13)
Sie kann nur für einige Randbedingungen analytisch gelöst
werden. Aufgelistet sind diese und weitere analytische Näherungslösungen in einem fundamentalen Werk von Carlslaw und Jaeger.
[6]
Eine besondere Bedeutung hat der Ausdruck 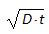 mit der Dimension "Länge". Er bezeichnet den Diffusionsweg für die Zeit t. Am Ort
mit der Dimension "Länge". Er bezeichnet den Diffusionsweg für die Zeit t. Am Ort
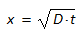 (14)
(14)
nimmt die Konzentration etwa die Hälfte der Gleichgewichtskonzentration an ( der genaue Wert ist fehlf(1/2)), wie aus der Fehlerfunktion Gleichung (13) mit Gleichung (14)hervorgeht, Gleichung (15).
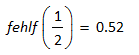 (15)
(15)
Die fundamentale Gleichung (14), in der Schreibweise
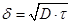 (16)
(16)
Relaxationsgleichung genannt, eignet sich gut, um Diffusionsvorgänge abzuschätzen. Hierin ist δ der Diffusionsweg, für den innerhalb der Zeitkonstanten τ die Hälfte der Ausgleichskonzentration erreicht ist.
Die Zeitkonstante wird als Relaxationszeit bezeichnet und ergibt sich aus der Relaxationsgleichung zu
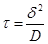 (17)
(17)
Mit Hilfe der Diffusionsgleichungen lassen sich unterschiedliche
werkstoffkundliche Phänomene erklären und beschreiben, so
Entfestigungsvorgänge durch Wärmebehandlung und Abläufe beim
Abkühlen von Schweißähten. Ausgang für die Betrachtung von
Wärmebehandlungen und bei Schweißvorgängen ist die zweite
Diffusionsgleichung. mit der Temperaturabhängigkeit der
Diffusionskonstanten.
Berechnungsbeispiel zur Diffusion
Betrachtet wird hier ein zeitlicher Verlauf der Diffusion von Kohlenstoff in α-Eisen mit der realitätsnahen Vorgabe, dass zwei Stahlsorten unterschiedlicher Kohlenstoffgehalte (cα = 0,4 % und cβ = 0,1 %) aber gleichen Diffusionskonstanten D = 10-10 m²/s, auf gleiche Temperatur erwärmt und dann in Kontakt gebracht werden. Die beiden Teile sind gleich lang und haben gleiche Querschnitte. Nach langer Zeit werden sich über den Diffusionsvorgang alle Konzentrationsunterschiede ausgeglichen haben und zwar auf den zwischen den Ausgangskonzentrationen gemittelten Wert. Der Kohlenstoffanteil aus dem Bereich mit höherer Konzentration sinkt, im anderen Bereich steigt er.
Diese Randbedingungen werden in die Integralform der zweiten Diffusionsgleichung (für den ebenen Fall mit der Zeit t und dem Ort x in einer Dimension, die x-Richtung), Gleichung (11), eingebracht und führen zur Formulierung Gleichung (18).
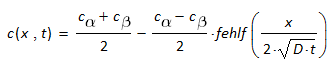 (18)
(18)
Diese kann numerisch gelöst werden und ergibt für verschiedene Zeiten Lösungen entsprechend der
Graphen Bild 5.
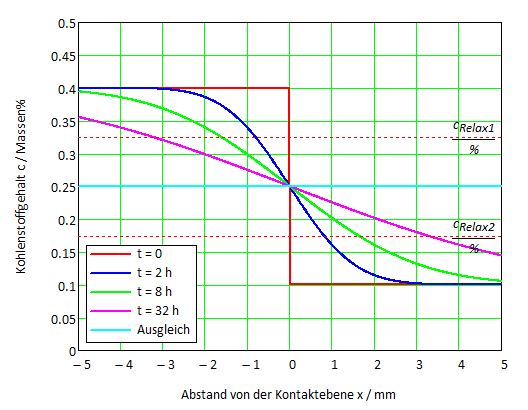
negative Abstände zur Kontaktebene, und 0,1 Massen% C, positive Abstände; D = 10 -10 m2 / s (entsprechend der Temperatur 1000 K); eindimensionaler Fall; die Teile berühren sich bei x = 0 zur Zeit t = 0; Parameter: Zeit.
Zu Beginn der Diffusion liegt ein Konzentrationssprung vor, dann diffundiert der Kohlenstoff aus immer größeren Tiefen des höher legierten Teils in immer größere Tiefen des niedriger legierten Teils. In der Kontaktfläche liegt nach dem Diffusionsstart eine mittlere Konzentration vor, die Ausgleichskonzentration. Im Endzustand (die Zeit geht gegen unendlich) ist die Konzentration im gesamten Stoff auf diese Ausgangskonzentration ausgeglichen.
Die Relaxations-Konzentration, das ist etwa die Hälfte des Konzentrationsunterschiedes (fehlf(1/2)) zwischen Start- und Ausgleichskonzentration, ist im linken Teil 0,328 % C – also etwa die Hälfte vom Ausgang zum Ausgleich – und im rechten Teil entsprechend 0,172 % C. Diese Konzentrationen werden jeweils nach den Relaxationszeiten erreicht. Für doppelte Diffusionswege werden vierfache Zeiten benötig, siehe auch Gleichung (17). Der Vergleich mit den Parametern veranschaulicht die Aussagekraft der Relaxationsgleichung.
5 PHASENUMWANDLUNG
Zunächst ist der Begriff "Phase" im Zusammenhang mit Stoffen zu definieren. Dort wird unter Phase ein zusammenhängender homogener Bereich mit gleichen physikalischen und chemischen Eigenschaften innerhalb einer Begrenzung, der Phasengrenze, verstanden.
Eine besondere Art der Phasen stellen dabei die Aggregatzustände dar. Alle Stoffe, die nicht nur Elementarteilchen sind, können in verschiedenen Aggregatzuständen vorliegen: Plasma, Gas, Flüssigkeit Festkörper. Verbunden damit sind auch verschiedene Ordnungszustände. Die Ordnung nimmt vom Plasma zum Festkörper zu. Die Festkörper selbst können, auch wenn sie nur aus einem (chemisch definierten) Stoff bestehen, unterschiedliche Ordnungszustände annehmen, die dann auch unterschiedliche Phasen darstellen. Als Beispiel sei hier in einem Werkstoff Stahl die Anordnung der Atome in kubisch raumzentrierten Kristalliten - genannt Alphaeisen - und nach einer thermischen Behandlung, dem Martensithärten, in tetragonal raumzentrierten verzerrten Kristalliten als Martensit vorliegen.
Ordnungszustände sind energetisch bestimmt und können reversibel oder irreversibel sein. Irreversibel ist beispielsweise der Ordnungszustand im Feststoff Acrylglas in die Gasform. Die Moleküle des Acrylglases zersetzen sich bei hohen Temperaturen, so dass sie sich nach Abkühlen nicht wieder in Acrylglas umwandeln. Eis als Feststoff unter Normaldruck schmilzt bei Erwärmung, verdampft und wird zum Plasma. Umgekehrt entsteht aus diesem Plasma bei Abkühlung wieder Eis.
Im Fachgebiet Materialbearbeitung mit Laserstrahlen spielt die Phasenumwandlung sowohl reversibler als auch irreversibler Art für die überwiegenden Bearbeitungsfälle eine bedeutende Rolle. Das Gebiet ist derart umfangreich, dass hier zum Einstieg lediglich auf die in den Referenzen angegebenen Fachbücer verwiesen wird.
6 Referenzen
[1] Hornbogen,
E.; Eggeler, G.; Werner, E: Werkstoffe; Aufbau und
Eigenschaften, Springer, Berlin u.a. 2008;
Bergmann, W.: Werkstofftechnik Teil 1: Grundlagen,
Teil 2: Anwendungen, Carl Hanser Verlag München, Wien
2008;
Berns, H.; Theisen, W.: Eisenwerkstoffe, Springer
Verlag, Berlin u.a., 2008;
Callister, W. D.: Fundamentals of Materials Science
and Engineering, John Wiley & Sons 2007
[2] O. Kubaschewski, C. B. Alcock, Metallurgical Thermochemistry. 5th edition, Pergamon Press 27, 2006
[3] isotrop bedeutet, dass alle Richtungen gleiche Eigenschaften haben
[4] Die Betrachtungen zur Diffusion beschränken sich in diesem Kapitel auf Werkstoffe.
[5] Bemerkung: Bei Verwendung der Aktivierungsenergie für ein Teilchen wird anstelle der universellen Gaskonstanten R die Boltzmannkonstante kB eingesetzt.
[6] Carlslaw, H. S; Jaeger, J. C.: Conduction of Heat in Solids, Oxford at the Claredon Press 1959