Der Laserstrahl als Werkzeug
 Bild 1: Zünden einer Zigarre im Glühlampenlicht
Bild 1: Zünden einer Zigarre im Glühlampenlicht
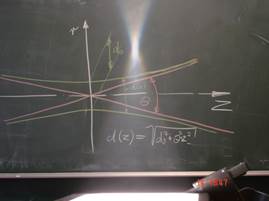 Bild 2: Ein fokussiertes Lichtbündel, sichtbar
Bild 2: Ein fokussiertes Lichtbündel, sichtbar
durch Zigarrenrauch.
Die Begrenzung ist ein
Hyperboloid.
Ein Werkzeug wird in Form und Gestalt an die ausgewählte Aufgabe angepasst. Das gilt auch für das optische „Werkzeug Laserstrahl“ mit seinen vielfältigen Einsatzmöglichkeiten in der Fertigung. Das Anpassen ist verhältnismäßig einfach. Lediglich einfache optische Komponenten wie die im Schreibprojektor, Bild 1, werden benötigt. Hier wird weißes Licht, das in einer Glühwendel erzeugt wird, über eine flache Linse (hier Fresnel-Linse) gebündelt. Zweck dieser Bündelung ist, dass das Licht aus der Quelle „Glühwendel“ möglichst vollständig durch eine Abbildungsoptik geführt werden kann. Im Bild ist die Abbildungsoptik zur Seite geschwenkt, so dass der engste Querschnitt des Bündels zugänglich wird. In diesem ist die Lichtleistung derart konzentriert, dass eine Zigarre zündet. Der Zigarrenrauch macht den Lichtweg sichtbar, Bild 2.
Deutlich erkennbar ist die Begrenzung des Lichtbündels in der Form eines einschaligen Hyperboloids. Dieser enthält immer einen engsten Querschnitt, die Strahltaille, auch Fokus genannt. Hier wurde also mit Hilfe optischer Komponenten aus einer Strahlquelle, der Glühwendel, ein Strahlen-bündel aus Licht geformt. Auf die gleiche Weise werden auch Strahlenbündel geformt, die ihren Ursprung in einem Laser als Strahlquelle haben – also Laserstrahlen.
Der Umfang, in dem sich Formung und andere Eigenschaften von Laserstrahlen verändern lassen, ist allerdings viel weiter als der von Glühlampenlicht. So können Leistungen bis in den Terawattbereich und Fokusdurchmesser bis hinab zu Nanometern eingestellt werden. Auf der einen Seite lassen sich sogar Grenzbedingungen einstellen, die lediglich durch die heute allgemein anerkannte Grenze der Physik eingeschränkt werden: durch die Unschärfe-Relation. Die andere Seite unterscheidet sich nicht von den allgemein bekannten Regeln im Umgang mit Licht oder anderen Strahlen.
Diese Vielfalt von einstellbaren Eigenschaften lässt Laserstrahlen zu verschiedensten Werkzeugen verwenden, die bei der Bearbeitung von Werkstoffen und anderen Materialien Vorteile gegenüber konventioneller Fertigungstechniken bringen können. Auch neue Produktionsverfahren sind möglich. Allerdings sollten dafür die Eigenschaften des Werkzeugs Laserstrahl bekannt sein. Dazu kann dieses Kapitel helfen.
Der Inhalt dieses Kapitels ist auf diejenigen Eigenschaften von Laserstrahlen beschränkt, die zum Verständnis der Materialbearbeitung mit Laserstrahlen in der Fertigungstechnik hilfreich sind. Der Laserstrahl als Werkzeug ergänzt die konventionellen Fertigungstechniken,ist aber heute noch nicht so bekannt, dass Möglichkeiten und Grenzen für seine Verwendung sicher beurteilt werden können. Daher wird hier auf die wesentlichen Eigenschaften eingegangen. Diese werden so behandelt, dass die Aussagen nachvollziehbar sind und sich aus eigenen Überlegungen heraus ergänzen lassen. Andererseits sind sie so umfangreich dargestellt, dass neue Ideen zur Auswahl von Laserstrahlen für besondere noch nicht verwirklichte Anwendungsmöglichkeiten gefunden werden können. Zum leichteren Einprägen sind die Regeln und Gesetzmäßigkeiten auch abgeleitet oder durch Anschauungen plausibel gemacht. Als Voraussetzung beim Leser genügen Kenntnisse im Umgang mit mathematischen Formalismen. Grundlegende physikalische Kenntnisse sind nützlich. Ohne diese können die Aussagen und Gesetze einfach hingenommen werden.
Die einzelnen Kapitel zum Laserstrahl als Werkzeug enthalten zum Nachvollziehen und zum Verständnis der Grundlagen eine Anzahl von Grafiken, Gleichungen und Referenzen. Diese sind hier in HTML-Kodierung mit CSS-Unterstützung nach dem Stand Januar 2017 eingebracht. Einige Bausteine lassen sich nicht so kodieren, dass sie in den verschiedenen Explorern gleich aussehen. Der Inhalt kann dadurch unübersichtlich werden. Aus diesem Grund ste
ht er zusätzlich als Laserstrahl PDF-Datei zur Verfügung.
1 Grundlegende Definitionen
Laserstrahl
Ein Laserstrahl ist ein Strahlenbündel[1]aus dem Bereich optischer Strahlung und Röntgenstrahlung, die in
einem Laser erzeugt wird. Diese Strahlung lässt sich als
Teilchenstrom und als elektromagnetische Welle betrachten
und beschreiben.[2]
Ein Laserstrahl unterscheidet sich von gewöhnlicher
optischen Strahlen unter anderem durch eine besondere
zeitliche und räumliche Kohärenz der Strahlung, sowie durch
die Monochromasie (Einfarbigkeit oder spektrale Breite, im
Frequenzbild: Bandbreite). Beide Größen können über
Laserstrahlen in Umfängen ausgewählt und reproduziert
werden, die mit anderen Strahlern nicht erreichbar sind.
Dazu kommt noch die Zeitdauer der Strahlung, die
reproduzierbar vom Femtosekundenbereich hin bis zur
kontinuierlichen Strahlung gesteuert werden kann. Für
Aufgaben in der industriellen Materialbearbeitung sind
außerdem von hohem Interesse die Strahlleistung und die
Bestrahlungsstärke (Leistungsdichte, Intensität)
Optische Strahlung
Optische Stahlung ist der Bereich der elektromagnetischen
Strahlung mit Wellenlängen λ für die gilt:
100 nm < λ < 1 mm.
Unterhalb von 100 nm schließt sich die Röntgenstrahlung an;
bei 1 mm beginnen die Mikrowellen.
Elektromagnetische Strahlung
hier als Welle beschrieben
[3]: Elektromagnetische Welle, deren
elektrische Feldstärke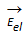 (und somit auch die über die Maxwellgleichungen eindeutig
verknüpfte magnetische Feldstärke
(und somit auch die über die Maxwellgleichungen eindeutig
verknüpfte magnetische Feldstärke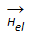 )
sich periodisch zeitlich und einsinnig räumlich ändert. In
den Betrachtungen bevorzugt wird die elektrische Feldstärke
)
sich periodisch zeitlich und einsinnig räumlich ändert. In
den Betrachtungen bevorzugt wird die elektrische Feldstärke 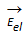 .
Die Ausbreitungsgeschwindigkeit ist die Lichtgeschwindigkeit
c. Die periodische Änderung wird durch die Periodendauer T, die Wellenlänge λ oder die
Frequenz ν gekennzeichnet. Der Zusammenhang
ist c = λ⋅ ν und ν = 1 / T .
.
Die Ausbreitungsgeschwindigkeit ist die Lichtgeschwindigkeit
c. Die periodische Änderung wird durch die Periodendauer T, die Wellenlänge λ oder die
Frequenz ν gekennzeichnet. Der Zusammenhang
ist c = λ⋅ ν und ν = 1 / T .
Für die Ausbreitungsgeschwindigkeit im Vakuum (und damit
näherungsweise auch in Luft im Normalzustand) gilt per
Definitionem: c = 2,99792458 108 m/s.
Anstelle der Feldstärken wird die Bestrahlungsstärke E (auch flächenbezogene Leistungsdichte E
oder Intensität I) betrachtet, da die Feldstärken praktisch nicht messbar sind und auch mit etwa ν = 1015 Hz oszillieren. Die Bestrahlungsstärke ist proportional zum
zeitlichen Mittelwert des Feldstärkenquadrates, Gleichung (1). Dieser zeitliche Mittelwert ist Messungen direkt
zugänglich.
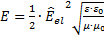 (1)
(1)
Hierin ist 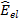 der Scheitelwert der elektrischen Feldstärke,
ε0 = 8,85418782 ⋅10-12 A⋅s / (V⋅m), die elektrische Feldkonstante, εr die Permittivitätszahl, μ0 =
4⋅π⋅10-7 V⋅s / (A⋅m) die magnetische Feldkonstante und μr die Permeabilitätszahl. Wenn anstelle des Scheitelwerts der elektrischen Feldstärke deren Effektivwert Eel betrachtet wird, dann gilt
der Scheitelwert der elektrischen Feldstärke,
ε0 = 8,85418782 ⋅10-12 A⋅s / (V⋅m), die elektrische Feldkonstante, εr die Permittivitätszahl, μ0 =
4⋅π⋅10-7 V⋅s / (A⋅m) die magnetische Feldkonstante und μr die Permeabilitätszahl. Wenn anstelle des Scheitelwerts der elektrischen Feldstärke deren Effektivwert Eel betrachtet wird, dann gilt
 .
.
Im Vakuum und näherungsweise auch in Luft gilt ε = 1 und μ = 1. Allgemein sind ε
und μ größer als 1. Sie definieren den
Brechungsindex n mit 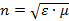 . In Materie
mit der Brechzahl n breitet sich das Licht mit der
Geschwindigkeit (Phasengeschwindigkeit) c1
= c / n aus. Diese ist im Allgemeinen niedriger als
die Vakuum-Lichtgeschwin-digkeit c. Weiterhin
gilt der Zusammenhang zwischen den Naturkonstanten: ε0 ⋅ μ0 = 1 / c 2. Die Bestrahlungsstärke E
ist ein Maß für die Leistungskonzentration und hat die
Dimension "Leistung durch Fläche".
. In Materie
mit der Brechzahl n breitet sich das Licht mit der
Geschwindigkeit (Phasengeschwindigkeit) c1
= c / n aus. Diese ist im Allgemeinen niedriger als
die Vakuum-Lichtgeschwin-digkeit c. Weiterhin
gilt der Zusammenhang zwischen den Naturkonstanten: ε0 ⋅ μ0 = 1 / c 2. Die Bestrahlungsstärke E
ist ein Maß für die Leistungskonzentration und hat die
Dimension "Leistung durch Fläche".
Kohärenz
Kohärent bedeutet "zusammenhängend". In der Praxis wird in
einem Lichtbündel dann Kohärenz festgestellt, wenn in dem
Bündel Interferenzen messbar (sichtbar) werden. Dazu dürfen
Wegunterschiede zwischen zwei Strahlwegen aus einer Quelle
bis zum Ziel eine gewisse Länge, die Kohärenzlänge, nicht
überschreiten. Wegunterschiede zweier aus einem Punkt
kommender Strahlen bestimmen die zeitliche Kohärenz (die
Zeit zum Erreichen des Zieles auf unterschiedlichen langen
Strahlwegen ist wegen der endlichen Lichtgeschwindigkeit
verschieden). Sonnenstrahlung (Sonnenlicht) lässt
Wegunterschiede in Längsrichtung bis etwa 3 µm noch zu,
um Interferenzen sichtbar zu machen. Das bedeutet, dass
Sonnenstrahlung aus Wellenzügen zusammengesetzt ist, die
etwa 3 µm lang sind. In Laserstrahlen können Wegunterschiede
zwischen Strahlen von Mikrometern bis zu vielen Kilometern
noch Interferieren. Zwischen beiden Grenzen lassen sich für
unterschiedlichste Aufgaben passende Laserstrahlen
auswählen. So wird eine große zeitliche Kohärenzlänge
geeigneter Laserstrahlen in Messaufbauten zum Nachweis von
Gravitationswellen eingesetzt.
Der seitliche Abstand zweier Punkte einer ausgedehnten
Strahlungsquelle, für den noch Interferenz beobachtet wird,
bestimmt die räumliche Kohärenz. [4]
Monochromasie
Strahlung mit genau einer Wellenlänge λ wird
als monochromatisch (einfarbig) bezeichnet. Diese Strahlung
ist, wie die Unschärfe-Relation zeigt, nicht herstellbar. Zu
jeder Wellenlänge λ gehört eine spektrale Bandbreite Δλ.
Diese ist mit der zeitlichen Kohärenzläng lt verknüpft: Δλ = λ2 / lt.
Bei einer Kohärenzlänge von 30 km eines
Laserstrahls der Wellenlänge 0,6 µm wäre das Verhältnis Δλ / λ = 2 ⋅ 10-11 ausgeprägt monochromatisch. Das Sonnenlicht
dagegen zeigt bei dieser Wellenlänge das Verhältnis Δλ / λ = 0,2. Damit ist das Sonnenlicht sehr breitbandig. Für Anwendungen in der
industriellen Materialbearbeitung spielt die Monochromasie
allerdings eine untergeordnete Rolle.
Verstärkungsmedium
Ein Verstärkungsmedium ist ein Stoff (freie Elektronen;
gasförmig; flüssig; fest), in welchem elektromagnetische
(optische) Strahlung verstärkt werden kann, in der Regel
dadurch, dass die Lebensdauer eines oberen (optischen)
Energieniveaus in dem Stoff größer ist als die eines
darunter liegenden. Wenn in dieses Medium Energie eingebracht wird, dann wird Besetzungsinversion und somit eine Verstärkung möglich, wie Einstein 1917 zeigte.
Optischer Resonator
Ein optischer Resonator als Bestandteil eines Lasers ist eine Einrichtung, die bewirkt, dass elektromagnetische Strahlung so geführt wird, dass sich die elektromagnetischen Felder reproduzieren. Im einfachsten Fall besteht der Resonator aus einer Faser als Lichtwellenleiter, deren Enden zusammengefügt sind. Wenn sich in ihr eine elektromagnetische Welle ausbreitet, dann läuft sie in der Faser um. Resonanz tritt dann auf, wenn sich die elektromagnetischen Felder nach einem Umlauf phasenrichtig schließen. Laser für die Materialbearbeitung enthalten anstelle einer sich schließenden Faser üblicherweise Resonatoren aus Spiegelsystemen.
Auskopplung
Ein Laserstrahl verlässt den Resonator über eine besondere
optische Einrichtung. Bei den meisten Lasern zur Verwendung
in der Materialbearbeitung wird dadurch ausgekoppelt, dass
einer der Resonatorspiegel teiltransparent ausgelegt ist.
Kurze Pulse werden auch durch schnell geschaltete
Einrichtungen unterschiedlichster Art (auch
Schall-Beugungsgitter) ausgekoppelt.
2 Eigenschaften des Laserstrahls
Ein Laserstrahl wird im Resonator geformt und aus dem
Laser ausgekoppelt, so dass er für Anwendungen verfügbar
ist. Er ist gekennzeichnet durch seine
- Wellenlänge (verbunden mit einer Bandbreite der
Wellenlänge), durch seine
- Leistung, die er mit sich führt, durch die
- Verteilung der Leistung über seinen Querschnitt,
durch die
- geometrische Form des Querschnitts, durch die
- Zeit, die er existiert, durch seine
- Durchmesser (oder Strahlabmessungen), durch seine
- Divergenz und durch die
- Änderung seiner Eigenschaften entlang des
Strahlweges.
Für Anwendungen in der Materialbearbeitung werden zwei
Typen von Laserstrahlen betrachtet: Laserstrahlen aus stabilen
Resonatoren, das sind Gaußstrahlen, und
Laserstrahlen aus instabilen Resonatoren, das sind
alle anderen Laserstrahlen. Sie unterscheiden sich
wesentlich bezüglich der Änderungen ihrer Eigenschaften
entlang des Strahlweges. Gaußstrahlen lassen sich einfacher
beschreiben, da sich ihre Charakteristik in
Ausbreitungsrichtung nicht verändert. Das gilt insbesondere
für die Leistungsverteilung über den Querschnitt. Diese
ändert sich entlang des Strahlweges nicht. In Laserstrahlen
aus instabilen Resonatoren dagegen hängt die
Leistungsdichteverteilung dagegen vom Ort auf dem Strahlweg
ab – so wie in gewöhnlichen Strahlenbündeln.
Allen Laserstrahlen gemeinsam ist, dass sie weder aus einem
Punkt kommen können noch ein Bündel paralleler Strahlen
darstellen. Das besagt die Unschärfe-Relation. Sie haben
aber immer eine engste Stelle, die Strahltaille, sowie eine
Divergenz, das heißt, der Strahldurchmesser ändert sich
entlang seines Strahlweges.
2.1 Gaußstrahlen
Für die meisten Lasertechnischen Materialbearbeitungsaufgaben kommen
Gaußstrahlen zum Einsatz. Diese vereinen zusätzliche
Vorteile von Laserstrahlen im Vergleich zu anderen Strahlen.
Gaußstrahlen werden in stabilen Resonatoren eines Lasers
erzeugt. [5]
Zunächst zum Begriff Laserresonator. Ein Laser-Resonator
ist ein optischer Resonator, in dem sich außerdem noch ein
Verstärkungsmedium befindet. Er enthält eine optische
Einrichtung zum Auskoppeln des Laserstrahls.
Ein optischer Resonator wird dann als stabil bezeichnet, wenn außerhalb der optischen Achse weitere Strahlwege existieren, auf denen
der Strahl den Resonator nicht verlässt. Das ist im
einfachsten Fall eine geschlossene Schleife einer
Lichtleitfaser. Damit ist ein Ringresonator aufgebaut. Ein
Ringresonator kann auch über (mindestens) drei Spiegel in
geeigneter Anordnung aufgebaut sein. Für Aufgaben in der
Materialbearbeitung sind lineare Resonatoren üblich. Diese
enthalten zwei gegenüberliegende Spiegel, beispielsweise
Kugelspiegel. Bei geeigneter Auswahl der Spiegel gibt es
Strahlwege auch außerhalb der optischen Achse, auf denen der
Strahl den Resonator nicht verlässt, obwohl er unter einem
Winkel zur optischen Achse verläuft, wie im Beispiel des
eines konfokalen Resonators, Bild 3. Hier fallen die
Brennpunkte beider Spiegel zusammen. Alle Strahlen (hier im
mathematischen Sinn), die in diesem Beispiel durch den
Brennpunkt eines Spiegels verlaufen, werden nach Reflexion
zu Parallelstrahlen, diese nach der nächsten Reflexion
wieder zu Brennstrahlen, verlassen also den Resonator nicht.
Der Resonator ist somit stabil.
 Bild 3: Verlauf eines ausgewählten Strahlwegs im konfokalen Resonator,
stabiler Grenzfall
Bild 3: Verlauf eines ausgewählten Strahlwegs im konfokalen Resonator,
stabiler Grenzfall
Der ausgekoppelte Laserstrahl (in diesem Beispiel wird der
Laserstrahl durch einen teiltransparenten Resonatorspiegel
aus dem Resonator ausgekoppelt) setzt sich somit aus
Teilstrahlen unterschiedlicher Richtungen zusammen. Das
führt zu Überlagerungen der Wellenfronten (Interferenzen)
und somit zu einer transversalen Modulation der
Leistungsdichte-Verteilung, das heißt zu einer höheren transversalen
Modenordnung
[6], in diesem Beispiel eine
transversale Modenordnung mit Spiegelsymmetrie. Ein
rotationssymmetrischer Verlauf der Strahlwege ist ebenso
möglich, Bild 4. Hier wird ein Strahl eines Zeigelasers in
einen Resonator aus einem Planspiegel und einem Kugelspiegel
(R = 2,5 m) im Tabakrauch sichtbar. Der Strahl wird
durch eine Bohrung in den Resonator eingeführt und
reproduziert sich nach acht Umläufen. Er verlässt den
Resonator also nie. Daher ist dieser stabil.
 Bild
4: Resonatormodell mit rotationssymmetrischem
Strahl-
Bild
4: Resonatormodell mit rotationssymmetrischem
Strahl-
verlauf. Hier wird ein Strahl eines Zeigelasers in einen
Resonator aus einem Planspiegel und einem Kugelspiegel
(R = 2,5 m) im Tabakrauch sichtbar. Der Strahl wird
durch eine
Bohrung in den Resonator eingeführt und reproduziert sich
nach acht Umläufen. Er verlässt den Resonator also nie.
Daher ist dieser stabil
Gaußstrahlen höherer transversaler Modenordnung haben eine
Invariante
[7], die größer ist als die
Untergrenze aus der Unschärfe-Relation [8];
denn sie werden mit Strahlverläufen außerhalb der optischen
Achse generiert. Lineare Resonatoren können ebenfalls aus
Fasern aufgebaut sein, deren Enden verspiegelt sind. In
diesen werden die transversalen Eigenschaften des Strahls
wesentlich über das Verhältnis zwischen dem Kerndurchmesser
der Faser zur Wellenlänge der Strahlung bestimmt.
Neben der transversalen Modenordnung geht auch die longitudinale
Modenordnung in die Beschreibung eines Gaußschen
Laserstrahls ein. Das ist die Anzahl der Wellenlängen, die
in einen Umlauf eines Wellenzuges in den Resonator passen.
In Anwendungen für die industrielle Materialbearbeitung ist
die longitudinale Modenordnung nahezu ohne Bedeutung.
Lediglich kurzzeitige Sprünge in der Ordnungszahl machen
sich bei einigen Anwendungen mit bestimmten Lasern im
Bearbeitungsergebnis bemerkbar. Auf die longitudinale
Modenordnung wird daher hier nicht weiter eingegangen.
2.1.1 Transversale Modenordnung
Grundeigenschaft eines (stabilen) Resonators ist die, dass
er ein Schwingungsfeld reproduziert. Dies ist auch in
optischen Resonatoren der Fall, also für elektromagnetische
Wellen. Diese passen nach einem Umlauf im Resonator mit
einer ganzzahligen Anzahl der Wellenlänge in den Umlaufweg
(doppelte Resonatorlänge). Die Anzahl wird "longitudinale
Modenordnung" genannt. Da elektromagnetische Wellen
senkrecht zur Ausbreitungsrichtung zweidimensional
ausgedehnt sind, erfordert das "Reproduzieren des
Wellenfeldes" zusätzlich, dass auch die Feldverteilung quer
zur Ausbreitung zweidimensional reproduziert wird. Im
einfachsten Fall ist das Feld quer zur Ausbreitung in beiden
Dimensionen gaußverteilt. Dieser einfachste Fall wird
transversaler Grundmode genannt, Bild 5.
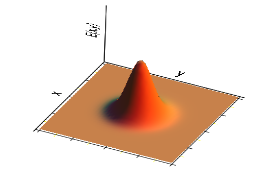 Bild 5:
Leistungsdichteverteilung im
Bild 5:
Leistungsdichteverteilung im
Grundmode
Weitere Feldverläufe, die auch in beliebig vielen Umläufen
reproduziert werden, sind über Polynome beschreibbar:
Hermite-Polynome bestimmen die Feldverteilung bei
Spiegelsymmetrie in Hermite-Gaußstrahlen, Bild 6, und
Laguerre-Polynome die der rotationssymmetrischen
Laguerre-Gaußstrahlen, Bild 7.
In diesen Darstellungen wurde eine der beiden orthogonalen
Dimensionen ausgewählt. In Hermite-Gauß-Strahlen nimmt die
zweite Dimension ebenfalls eine Hermite-Gauß-Funktion ein.
Diese ist unabhängig von der ersten. In den
rotations-symmetrischen Laguerre-Gauß-Strahlen moduliert die
Ordnung der zweiten Dimension die Feldstärke in
Umfangrichtung.
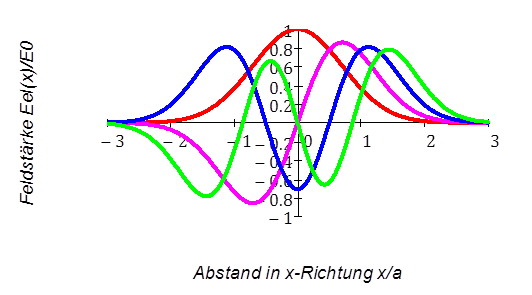 Bild 6:Feldverteilung in transversalen
Hermite-Gauß-Moden der Ordnung TEM00 bis TEM 03 (rot,
violett, blau, grün) in der Ebene x-Strahlachse. Die
Feldstärke ist normiert auf das Grundmode-Maximum, die
Anzahl der Nulldurchgänge entspricht der Polynom-Ordnung
und zeigt die Modenordnung in der Ebene an.
Bild 6:Feldverteilung in transversalen
Hermite-Gauß-Moden der Ordnung TEM00 bis TEM 03 (rot,
violett, blau, grün) in der Ebene x-Strahlachse. Die
Feldstärke ist normiert auf das Grundmode-Maximum, die
Anzahl der Nulldurchgänge entspricht der Polynom-Ordnung
und zeigt die Modenordnung in der Ebene an.
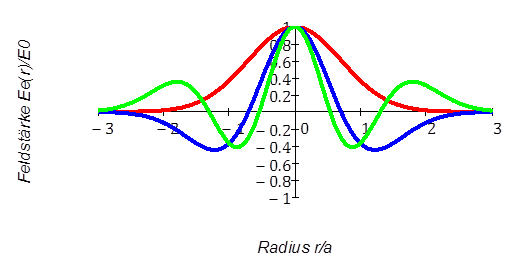
Bild 7: Feldverteilung in transversalen
Laguerre-Gauß-Moden der Ordnung TEM00 bis TEM 02 (rot,
blau, grün) in der Ebene Radius-Strahlachse. Die
Feldstärke ist normiert auf das Grundmode-Maximum, die
Anzahl der Nulldurchgänge entspricht der Polynom-Ordnung
und zeigt die Modenordnung Radius-Richtung an
Durch Quadrieren und Normieren der Feldstärkefunktionen
ergibt sich die Verteilung der Leistungsdichte.[9]
Der Strahl wird breiter, das Maximum der Leistungsdichte
verschiebt sich in Hermite-Moden mit höherer Ordnung nach
außen, Bild 8. In Laguerre-Moden bleibt das Maximum mit der
Leistungsdichte des Grundmodes im Zentrum des Strahles. Die
Verbreiterung des Gesamtstrahls erfolgt auf Kosten des
inneren Bereichs. Dieser wird schmaler, Bild 9.
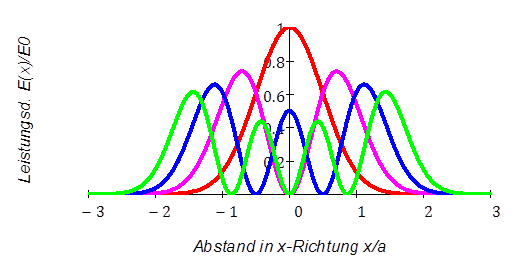 Bild 8:Leistungsdichte-Verteilung in
transversalen Hermite-Gauß-Moden der Ordnung TEM00 bis
TEM 03 (rot, violett, blau, grün)in der Ebene X -
Strahlachse. Die Leistungs-dichte ist normiert auf das
Grundmode-Maximum.
Bild 8:Leistungsdichte-Verteilung in
transversalen Hermite-Gauß-Moden der Ordnung TEM00 bis
TEM 03 (rot, violett, blau, grün)in der Ebene X -
Strahlachse. Die Leistungs-dichte ist normiert auf das
Grundmode-Maximum.
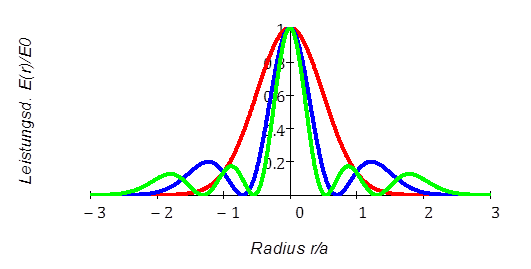 Bild 9: Leistungsdichte-Verteilung in
transversalen
Bild 9: Leistungsdichte-Verteilung in
transversalen
Laguerre-Gauß-Moden der Ordnung TEM00 bis TEM 02
(rot, blau, grün)in der Ebene Radius-Strahlachse.
Die Leistungsdichte ist normiert auf das
Grundmode-Maximum.
Einen Eindruck zur Verteilung der Leistungsdichte im
Querschnitt von Laserstrahlen mit niedriger Modenordnung
vermitteln die Berechnungen in Bild 10 und Bild 11.
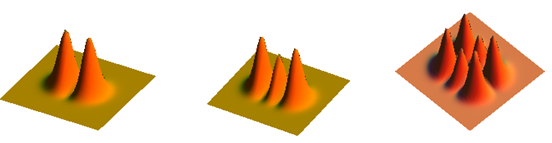 Bild 10: Leistungsdichte-Verteilung in
Hermite-Moden TEM01, TEM02 und TEM21
Bild 10: Leistungsdichte-Verteilung in
Hermite-Moden TEM01, TEM02 und TEM21
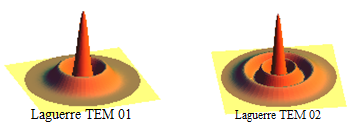 Bild 11: Leistungsdichte-Verteilung in Laguerre-Moden
TEM01 und TEM02.
Bild 11: Leistungsdichte-Verteilung in Laguerre-Moden
TEM01 und TEM02.
Der erste Index zeigt an, dass keine Modulation in
Umfangsrichtung auftritt.
Die hier gezeigten Moden können sich in Laserstrahlen
überlagern oder auch mit hoher Frequenz wechseln, so dass
der zeitliche Mittelwert wahrgenommen wird.
 Bild
12: Ringmode aus der Überlagerung
Bild
12: Ringmode aus der Überlagerung
der Transversalmoden TEM01 mit TEM10
Eine besondere Überlagerung von Hermite-Moden wird in
einigen Anwendungen zur Materialbearbeitung gezielt
ausgewählt: die Überlagerung eines Hermite-Modes der Ordnung
TEM01 mit dem Hermite-Mode TEM10, Bild 12. Hierin überlagern
sich zwei orthogonal orientierte Moden gleicher Ordnung, die
in Addition der Leistungsdichte zu einem Ring führen.
Derartige Überlagerungen werden in der Indizierung mit einem
Stern gekennzeichnet und Ringmode genannt. Das Beispiel
zeigt den Mode TEM01*.
2.2 Andere Strahlen
Laser mit sehr hohen Leistungen verwenden auch instabile
Resonatoren und koppeln den Strahlanteil aus, der an einem
Resonatorspiegel seitlich auswandert, Bild 13. Ein Vorteil
dieser instabilen Resonatoren ist der, dass die in den
Resonator eingebrachte Leistung aus dem ganzen Volumen zum
Aufbau des Laserstrahls beiträgt.
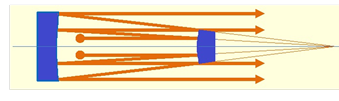 Bild
13: Instabiler Resonator, Beispiel für den Verlauf
ausge-
Bild
13: Instabiler Resonator, Beispiel für den Verlauf
ausge-
wählter Strahlwege im konfokalen Resonator, instabiler
Grenzfall
Zum anderen liegt im Resonator selbst kein engster
Strahlquerschnitt, in dem dann bei hohen Leistungen die sehr
hohen Leistungsdichten Komponenten des Resonators
beschädigen oder zerstören würden.
Nachteilig bei Strahlen aus instabilen Resonatoren ist
allerdings, dass sich entlang des Strahlverlaufes die Art
der Leistungsverteilung ändert. Direkt vor dem
Resonatorausgang ist die Leistung im rotationssymmetrischen
Strahl ringförmig um die Strahlachse verteilt. Weit entfernt
dagegen, im "Fernfeld" liegt in der Stahlachse ein Maximum
der Leistungsdichte vor, umgeben mit ringförmigen Bereichen
geringerer Leistungsdichte. Physikalisch (mathematisch)
betrachtet stellt das "Fernfeld" die Furier-transformierte
Leistungsdichteverteilung des Strahlquerschnitts am Ausgang
dar. Ein weiterer Nachteil ist, dass sich mit der
Strahlleistung am Resonatorausgang die Ringbreite und die
Verteilung der Leistungsdichte im Ring ändern. Damit ändert
sich auch die Leistungsdichteverteilung im "Fernfeld"
abhängig von der Strahlleistung. Ein "Fernfeld" liegt auch
im Fokus hinter einer Fokussieroptik vor.[10]
Aus diesem Grunde werden Strahlen aus instabilen
Resonatoren für Anwendungen in der industriellen
Materialbearbeitung nur dann verwendet, wenn sehr hohe
Leistungen gefordert sind. Dafür wurden bereits Laser mit 90
kW kontinuierlicher Strahlleistung eingesetzt. Eine
besondere Ausführung von Hochleistungslasern verwendet
Resonatoren, die in einer Querrichtung (der
Strahlquerschnitt ist zweidimensional) stabil und in der
anderen instabil ausgelegt sind. Damit wird eine hohe
Strahlleistung in der instabilen transversalen Richtung aufgebaut und mit Eigenschaften von stabilen Resonatoren in der anderen Richtung verbunden.
2.3 Laserstrahl-Durchmesser
Laserstrahlen sind nicht scharf begrenzt wie Drähte oder
Wasserstrahlen. In einem Grundmode-Laserstrahl[11]
beispielsweise verteilen sich die Leistungsanteile über den
Strahlquerschnitt symmetrisch zur Strahlachse entsprechend
einer Gaußschen Glockenkurve. Diese strebt erst im
unendlichen Abstand von der Achse gegen null. Der
Laserstrahl ist daher unscharf begrenzt.
Da der Strahlquerschnitt zweidimensional ist und im
Allgemeinen nicht kreisrund, sind zudem zwei Angaben für die
Beschreibung seiner Ausdehnung nötig. Diese werden dann Strahlabmessungen
genannt. Nur im Spezialfall des rotationssymmetrischen
Strahlquerschnitts reicht die Angabe eines
Strahl-Durchmessers aus. Der Übersichtlichkeit wegen werden
in diesem Kapitel zunächst rotationssymmetrische
Stahlquerschnitte betrachtet.
Wegen der unscharfen Begrenzung der Laserstrahlen werden die
Durchmesser über ihre "physikalischen Größen" definiert.
Hierzu werden besondere Kriterien ausgewählt, wie eine
bestimmte Leistungsdichte (Bestrahlungsstärke), oder auch
der Leistungsanteil, der durch einen begrenzenden
Querschnitt oder durch begrenzende Abmessungen hindurch
fließt.
Zunächst zur Leistungsdichte (Bestrahlungsstärke).
Diese physikalische Größe wird im Gebiet der Optik als
Bestrahlungsstärke E definiert, da der Begriff
Dichte auf das Volumen bezogen genormt war. In der
Lasertechnik wird der Begriff Leistungsdichte als
Flächen-bezogene Größe verwendet. Falls Verwechslungen mit
dem gleichen auf das Volumen bezogenen Begriff möglich sind,
wird der Bezug zusätzlich angegeben. Die (flächenbezogene)
Leistungsdichte E ist definiert als Quotient des
Leistungsanteils 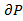 , der durch ein
Flächenelement
, der durch ein
Flächenelement 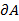 normal
hindurchtritt:
normal
hindurchtritt:
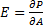 (2)
(2)
Ausgang für eine Definition des Durchmessers ist der
rotationssymmetrische Grundmode-Laserstrahl. Dies ist ein
ausgezeichneter Laserstrahl, nämlich derjenige, der die
untere Grenze der Heisenbergschen Unschärfe-Relation [12]
erreicht. In ihm ist die Leistungsdichte über den
Querschnitt gaußförmig verteilt. Zunächst zur
Gaußverteilung: Die Funktion einer Gaußverteilung in
einfachster mathematischer Form in einer x-y-Ebene
ist:
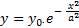 (3)
(3)
wobei a der Parameter dieser Gaußfunktion ist und y0
das Maximum bei x = 0. Der Parameter a zeigt
die Breite der Gaußschen Glockenkurve im Verhältnis zur Höhe
an. Gleichung (3) zeigt, dass die Höhe der Kurve bei
x = a den Betrag 1/e des Maximums annimmt, Gleichung (4).
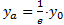 (4)
(4)
Übertragen auf physikalische Größen eines
rotationssymmetrischen Laserstrahls verläuft die Amplitude
der elektrischen Feldstärke Eel
entsprechend der Gaußfunktion. Diese ist dann für
rotationssymmetrische Verteilung im Polarkoordinatensystem (r,φ)
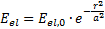 (5)
(5)
wobei r den Radius bezeichnet und a den
Strahlparameter. Diese elektrische Feldstärke ist wegen der
hohen Frequenzen der optischen Strahlung nur schwer messbar
und wird daher auf die Leistungsdichte E
transformiert (E ∝ Eel2,
Gleichung (1)). Somit beschreibt sich die Verteilung
der Leistungsdichte E im Strahl über eine Quadrieren
der Gleichung (5) zu
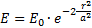 (6)
(6)
Der Anteil des konstanten Terms aus Gleichung (1) geht in
E0 ein. Aufgrund der Quadrierung
bezeichnet a den Ort im Strahl, auf dem die
Leistungsdichte auf 1/e2 des Maximums in
der Strahlachse abgesunken ist, Gleichung (7) und Bild 14.
Der Strahldurchmesser d ist damit d = 2a.
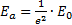 (7)
(7)
Allerdings sollte beachtet werden, dass in theoretischen
Ableitungen zur Beschreibung eines Laserstrahls auch andere
Durchmesser-Definitionen verwendet werden. So hat Heisenberg
in seiner Unschärfe-Relation den Wendepunkt der
Gaußverteilung betrachtet. Der Unschärfe-Relation lag die
Wahrscheinlichkeitsrechnung zugrunde. Der Wendepunkt
definiert die Standardabweichung σ. Weitere noch
übliche Durchmesser-Definitionen sind:
"Halbwertdurchmesser", der "Durchmesser im Wendepunkt" (2 ⋅
σ ), der "1/e - Durchmesser" und der "1/e2
- Durchmesser", Bild 14.
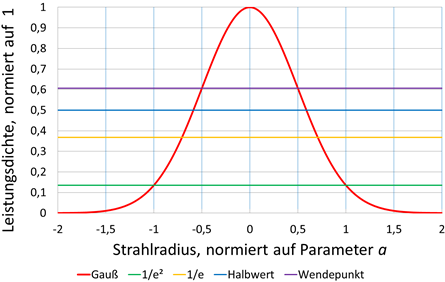 Bild 14: Zur Umrechnung unterschiedlicher
Durchmesserbezüge in einem Grundmode-
Bild 14: Zur Umrechnung unterschiedlicher
Durchmesserbezüge in einem Grundmode-
Laserstrahl Die Breite der Gaußschen Glockenkurve ist auf
den "1/e2-Wert" und die
Leistungsdichte auf das Maximum normiert. Die Geraden
kennzeichnen die normierten
Leistungsdichten für die unterschiedlichen
Durchmesser-Definitionen.
Diese Durchmesser lassen sich wie folgt umrechnen, Tabelle
1:
Tabelle 1: Umrechnung von gebräuchlichen
Durchmesser-Definitionen
|
Durchmesser 1/e2
|
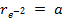
|
d
|
|
Durchmesser im Wendepunkt
|
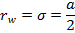
|
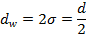
|
|
Halbwertdurchmesser
|
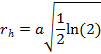
|
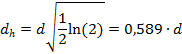
|
|
1/e-Wert
|
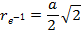
|
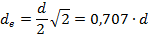
|
Für andere Gaußstrahlen[13],
das sind Laserstrahlen aus stabilen Resonatoren mit nicht
gaußförmiger Verteilung der Leistungsdichte (Laserstrahlen
mit einer höheren Ordnung von Transversalmoden), wird ein
Durchmesser ebenfalls auf den Wert 1/e² der Leistungsdichte
bezogen. Allerdings ist eine derartige Definition dann
unsicher, wenn die Randbereiche flach abfallen, wie in
höheren Laguerre-Moden[14],
Bild 15.
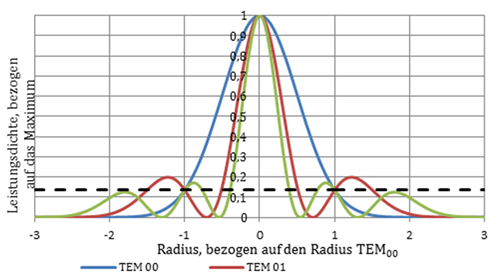 Bild 15:
Verlauf der Leistungsdichte in rotationssymmetrischen
Laserstrahlen der
Bild 15:
Verlauf der Leistungsdichte in rotationssymmetrischen
Laserstrahlen der
Modenordnung Laguerre TEM01 und TEM02
im Vergleich zum Grundmode, Normierung
auf die Gesamtleistung eines rotationssymmetrischen
Strahls; zur Durchmesser-
Bestimmung ist die Leistungsdichte Egrenz
= E0 / e2
eingetragen. Diese zeigt für die
höheren Modenordnungen jeweils mehrere Durchmesser an. Sie
ist nicht eindeutig
und sollte hier nicht gewählt werden.
Für diese Modenordnungen könnte die erste Nullstelle als
Durchmesserangabe gewählt werden. Dies wäre vorteilhaft für
Bearbeitungsaufgaben, bei denen die Leistungsdichte
maßgeblich ist.
Für andere Aufgaben in der Materialbearbeitung steht der
Leistungseintrag (aus der Energiebilanz) im Vordergrund. In
diesem Fall wäre beispielsweise bei höheren Modenordnungen
die bloße Angabe eines Durchmessers allein nur selten
ausreichend. So würde beispielsweise mit einem Laguerre
TEM02 Mode, siehe Bild 15, der recht erhebliche
Leistungsanteil außerhalb der ersten Nullstelle nicht
berücksichtigt.
In diesem Fall ist es sicherer, wenn der Durchmesser über
den Leistungsanteil bestimmt wird, der innerhalb eines
ausgewählten Querschnittes fließt. Dieser Leistungsanteil
wird dabei so gewählt, dass er mit der Definition des
Durchmessers über die Leistungsdichte bei Gaußverteilung
übereinstimmt. Die Entsprechung errechnet sich aus der
Definition der Leistungsdichte: 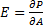 .
.
Durch Integration der Leistungsdichte über den ausgewählten
Strahlquerschnitt ist somit die Leistung P bekannt,
welche durch diesen Querschnitt begrenzt wird. Diese
berechnet sich bei Rotationssymmetrie zu
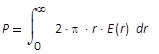 (8)
(8)
Und mit Gleichung (6) wird daraus Gleichung (9)
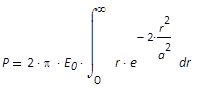 (9)
(9)
Integriert wird von null bis unendlich; damit wird hier
die Gesamtleistung des rotationssymmetrischen
Laserstrahls erfasst. Innerhalb des Durchmessers d
(d = 2 a) fließt lediglich der Leistungsanteil
Pa. Für diesen wird nur bis zur Obergrenze
a integriert.
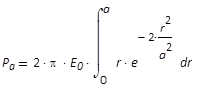 (10)
(10)
Das Verhältnis Pa / P
beträgt dann im Grundmode-Laserstrahl 0,865, Gleichung (11).
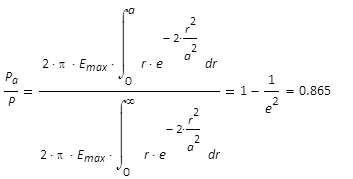 (11)
(11)
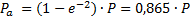 (12)
(12)
Somit lässt sich in rotationssymmetrischen Strahlen mit
Gauß-verteilter Leistungsdichte der 1/e2-Durchmesser
über den Leistungsanteil ermitteln, der konzentrisch zur
Strahlachse innerhalb einer Kreisblende hindurchtritt, Bild 16.
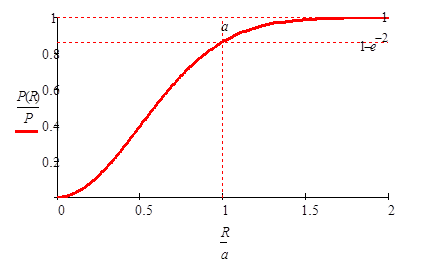 Bild
16: Berechnung des Leistungsanteils P(R),
der durch einen rotations-
Bild
16: Berechnung des Leistungsanteils P(R),
der durch einen rotations-
symmetrischen Grundmode-Laserstrahl innerhalb eines Radius
R fließt.
Die 1/e2 - Grenze ist eingezeichnet. Sie
schneidet die Leistungskurve
beim 1/e² - Durchmesser (Radius a) und zeigt den
Leistungsanteil
1-1/e² = 0,865 an.
Von zusätzlichem Interesse ist die Leistungsdichte E0
im Zentrum wenn Leistung P und Durchmesser d
des Strahls bekannt sind. Aus der Gaußverteilung eines
rotationssymmetrischen Strahlquerschnitts errechnet sich
diese aus Gleichung (9) wie folgt:
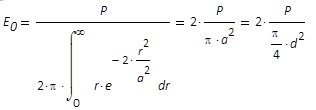 (13)
(13)
Hierin ist 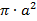 oder
oder 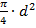 der Kreisquerschnitt
innerhalb des Durchmessers d. Die Leistungsdichte im
Zentrum entspricht somit der doppelten mittleren
Leistungsdichte, welche die Gesamtleistung auf den
Querschnitt innerhalb des Durchmessers d bezieht,
Gleichung (14).
der Kreisquerschnitt
innerhalb des Durchmessers d. Die Leistungsdichte im
Zentrum entspricht somit der doppelten mittleren
Leistungsdichte, welche die Gesamtleistung auf den
Querschnitt innerhalb des Durchmessers d bezieht,
Gleichung (14).
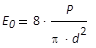 (14)
(14)
Für die höheren rotationssymmetrischen transversalen
Modenordnungen, siehe Bild 14, errechnet sich der
Leistungsanteil entsprechend, Bild 17. Hier sind die
Ordnungen Laguerre TEM00, TEM01 TEM02 und TEM03 dargestellt
sowie die 0,865-Anteil-Gerade (1 - e -2).
Ein Vergleich dieser über die Leistung ermittelten
Durchmesser führt zur Näherungsformel für höhere
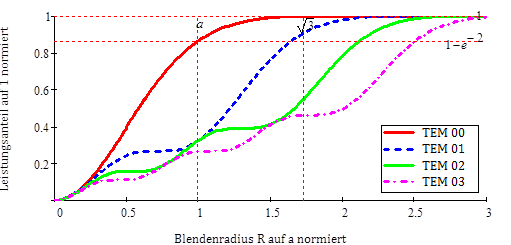
Laguerre-Modenordnungen TEM0n: 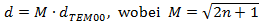 . Diese Übereinstimmung
ist grob, Bild 17, (
. Diese Übereinstimmung
ist grob, Bild 17, (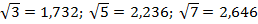 ).
). 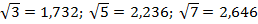
 Bild
17: Verlauf des Leistungsanteils in
rotationssymmetrischen Laserstrahlen der Modenordnungen
Bild
17: Verlauf des Leistungsanteils in
rotationssymmetrischen Laserstrahlen der Modenordnungen
TEM00,Laguerre TEM01, TEM02, und TEM03; Normierung der
Leistung jeweils auf die Gesamtleistung.
Zur Durchmesserbestimmung ist der Leistungsanteil 0,865
eingetragen.
Das Messen von Strahldurchmessern über eine Kreisblende
erfordert einen hohen Aufwand, da im ersten Schritt die
Kreisblende in zwei Dimensionen auf die (nicht zugängliche
unsichtbare) Strahlachse zentrierte werden muss. Leichter
ist das Messen über eine lineare Blende, die quer durch den
Strahl, beispielsweise in x-Richtung, geführt wird.
Anfangs deckt sie den Strahl voll ab. Dann wird sie weiter
geführt und mehr und mehr des Strahlquerschnitts
freigegeben. Der Verlauf der Leistung hinter der Blende wird
gemessen. Das Verfahren kommt insbesondere auch den
Anforderungen aus mehreren industriellen Anwendungsfällen
entgegen, bei denen der Laserstrahl in einer Linie über das
Werkstück geführt wird.
Für die physikalische Betrachtung legt eine lineare Blende
Berechnungen in kartesischen Koordinaten nahe. In
einem rotationssymmetrischen Laserstrahl mit gaußförmiger
Verteilung der Leistungsdichte wird dazu die Gesamtleistung
P somit durch Integration der Leistungsdichte über
die gesamte Ebene (in x- und y-Richtung) ermittelt,
Gleichung (15).
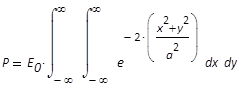 (15)
(15)
Wird hierin E0 substituiert (aus
Gleichung (14)), so nimmt der Leistungsanteil P(X),
der an der linearen Blende vorbei bis zur Position X fließt,
stetig zu, Gleichung (16) mit Bild 18.
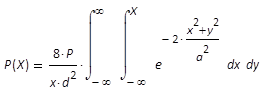 (16)
(16)
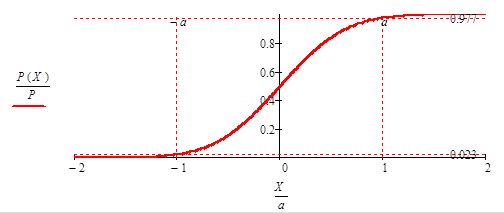 Bild
18: Anteil der Leistung eines rotationssymmetrischen
Grundmodestrahls, der an einer in
Bild
18: Anteil der Leistung eines rotationssymmetrischen
Grundmodestrahls, der an einer in
y - Richtung unendlich ausgedehnten linearen Blende
vorbei bis zur Position X durch den Strahl
verläuft, normiert auf den Strahlparameter a
Damit ist ein Weg beschrieben, den Stahldurchmesser über
das Hindurchführen einer Schneide zu bestimmen: Von großem
Abstand ausgehend, durch den Strahl hindurch gibt die
Schneide an Position -a den Leistungsanteil P-a / P = 0,023 frei, Gleichung (17)
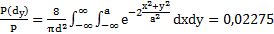 (17)
(17)
2,3 % der Leistung treten also in das Leistungsmessgerät.
Mit weiterer Führung zur gegenüberliegenden Position +a
der Strahlbegrenzung tritt der Anteil Pa
/ P = 0,977 (97,7 %) hindurch. Innerhalb einer
Strahlabmessung, also in den Grenzen -a bis +a
verlaufen somit 0,954 (95,4 %) der Gesamtleistung, Gleichung (18).
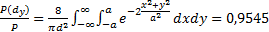 (18)
(18)
Dies Messverfahren eignet sich insbesondere auch zur
Beschreibung von nicht-rotationssymmetrischen Laserstrahlen.
Die Strahlbegrenzungen werden dann Strahlabmessungen
genannt. Gaußstrahlen mit höherer Hermite-Modenordnung TEMmn
sind im Allgemeinen nicht rotationssymmetrisch. Für deren
Strahlabmessungen gilt die Näherung 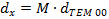 mit
mit 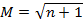 .
.
Die jeweils verwendeten Definitionen des Durchmessers eines
Laserstrahls werden auch zur Ermittlung der Divergenz
des Laserstrahls angewandt. Diese Größe "Divergenz" wird im
Kapitel 3 Strahlausbreitung behandelt. Sie beruht auf
der Bestimmung und somit auf der Definition von
Durchmessern, ist aber nur im Zusammenhang mit der
Strahlausbreitung, also über den Verlauf des Laserstrahls im
Raum, verständlich.
2.3.1 Strahlabmessungen
Laserstrahlen müssen nicht rotationssymmetrisch verlaufen.
Dies wird besonders deutlich, wenn die
Leistungsdichte-Verteilung im Strahlquerschnitt über
transversale Hermite-Moden bestimmt wird. Von daher können
in einem Strahlquerschnitt je nach Richtung unterschiedliche
"Strahldurchmesser" auftreten - auch im Grundmode mit
Verteilung der Leistungsdichte entsprechend Gaußschen
Glockenkurven in zwei orthogonalen Querschnittsrichtungen.
In diesem Fall hat der Strahl dann einen elliptischen
Querschnitt mit einem minimalen und einem maximalen
Durchmesser. Diese Durchmesser (Ellipsenachsen) stehen
senkrecht aufeinander und werden Strahlabmessungen dx
und dy genannt. Die Gesamtleistung
ergibt sich analog zum rotationssymmetrischen Strahl aus der
Leistungsdichte-Verteilung.
Die beiden Strahlabmessungen dx und
dy werden entweder aus der
Leistungsdichte bestimmt, als Abstand der im Strahl
gegenüberliegenden Orte, auf denen die Leistungsdichte 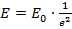 beträgt oder über den Leistungsanteil, der innerhalb zweier
linearer Begrenzungen hindurchtritt. Dieser ergibt sich
analog zu Gleichung (16) und Bild 18, wenn anstelle des
einen Parameters a die beiden Ellipsenparameter
(Halbachsen) a und b betrachtet werden.
beträgt oder über den Leistungsanteil, der innerhalb zweier
linearer Begrenzungen hindurchtritt. Dieser ergibt sich
analog zu Gleichung (16) und Bild 18, wenn anstelle des
einen Parameters a die beiden Ellipsenparameter
(Halbachsen) a und b betrachtet werden.
Die
Gesamtleistung P im Strahl mit Gaußverteilung der
Leistungsdichte und der maximalen Leistungsdichte E0
im Zentrum ist analog zu Gleichung (15):
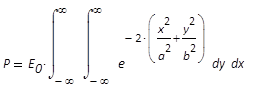 (19)
(19)
Diese Integration der Leistungsdichte über die gesamte
Ebene, durch den Laserstrahl führt zur Gesamtleistung P = 1/2 ⋅π⋅a⋅b⋅E0. Also nimmt die zentrale Leistungsdichte auch im elliptischen Querschnitt
eines Strahls im Grundmode den doppelten Wert der mittleren
Leistungsdichte an (bezogen auf die Ellipse mit der
Begrenzung a und b; die Fläche
einer Ellipse ist a⋅b⋅π)
2.3.2 Messverfahren mit linearer Schneide
Zum Messen der Strahlabmessungen eines elliptischen
Laserstrahls wird eine linear begrenzte Blende in Richtung
der Hauptachsen (Minimal- oder Maximaldurchmesser) durch den
Laserstrahl geführt. Diese ist senkrecht zur
Bewegungsrichtung ausgedehnt ist und deckt den Strahl
zunächst vollständig ab. Bei Führung in x-Richtung
wird abhängig von der Position X der Leistungsanteil
P(X) freigeben entsprechend
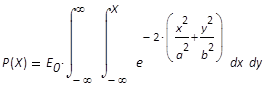 (20)
(20)
Die Lösung dieser Gleichung führt zu
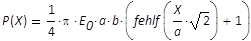 (21)
(21)
Von Interesse ist nun die Frage nach dem Anteil der
Leistung, die zwischen den Begrenzungen des Strahls -a und +a
hindurchtritt. Dazu wird aus Gleichung (21) der
Leistungsanteil P(x = a) für x =
a bestimmt:
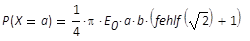 (22)
(22)
Bezogen auf die Gesamtleistung ist das Verhältnis
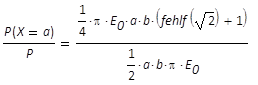 und somit
und somit
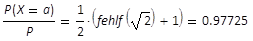 (23)
(23)
In der Blendenposition X = -a errechnet sich der
Leistungsanteil entsprechend zu
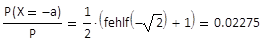 (24)
(24)
Zwischen den Grenzen -a und +a verläuft der
Leistungsanteil
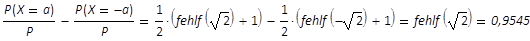 (25)
(25)
das heißt, außerhalb der Strahlgrenzen -a und +a
werden jeweils die Anteile 0,02275 (2,3 %) ausgeblendet.
Innerhalb der linearen Begrenzung an den Strahlabmessungen
verlaufen somit 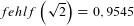 der
Gesamtleistung. Das ist der gleiche Anteil, der im
rotationssymmetrischen Strahlquerschnitt innerhalb des
Durchmessers hindurchtritt, Gleichung (25). Die
gleichen Betrachtungen gelten ebenso für die orthogonale
Richtung mit dem Ellipsen-Parameter b.
der
Gesamtleistung. Das ist der gleiche Anteil, der im
rotationssymmetrischen Strahlquerschnitt innerhalb des
Durchmessers hindurchtritt, Gleichung (25). Die
gleichen Betrachtungen gelten ebenso für die orthogonale
Richtung mit dem Ellipsen-Parameter b.
2.4 Zusammenfassung der Aussagen zum
Laserstrahldurchmesser
und zu den Strahlabmessungen
Die in dieser Zusammenfassung verwendeten Bezeichnungen
weichen zum Teil von den in DIN angegebenen ab, da in diesem
Kapitel einfache nachvollziehbare physikalische Grundlagen
verwendet werden.
In rotationssymmetrischen Strahlen wird der
Durchmesser bestimmt
- über den Abstand zwischen zwei gegenüberliegenden Orten,
in denen die Leistungsdichte 1/e² des Maximums beträgt
- über den Leistungsanteil
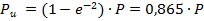 , der durch eine Kreisfläche um die
Strahlachse mit dem Durchmesser du hindurchtritt. Hier ist
u = 0,865 = 86 %, also d86,5
, der durch eine Kreisfläche um die
Strahlachse mit dem Durchmesser du hindurchtritt. Hier ist
u = 0,865 = 86 %, also d86,5
- über einen ausgewählten Leistungsanteil Pu
mit dem Index u, beispielsweise d50 für den
Anteil 50 % der Gesamtleistung, dies entspricht bei
Gaußverteilung dem Halbwertdurchmesser.
- Bei Messungen über lineare Blenden wird die Messrichtung
indiziert, beispielsweise dx,u, wobei
mit x die Ausdehnung in x-Richtung indiziert wird
und mit u = 0,954 bei Gaußverteilung der 1/e² -
Bezug getroffen wird,
- durch weitere Angaben wie der Ort des ersten Minimums
oder eines bestimmtes Maximums der Leistungsdichte
In nicht rotationssymmetrischen Stahlquerschnitten werden Strahlabmessungen
in zwei orthogonalen Richtungen minimaler und maximaler
Ausdehnung bestimmt, wobei deren Richtungen durch Indices x
und y gekennzeichnet sind,
- über den Abstand zwischen zwei gegenüberliegenden Orten
in maximaler und minimaler Ausdehnung des Querschnitts, in
denen die Leistungsdichte 1/e² des Maximums beträgt
- über den Leistungsanteil Pu =0,954 P,
der durch zwei lineare Begrenzungen im Abstand dx oder dy
hindurchtritt, wobei außerhalb beider Grenzen jeweils die
Anteile 0,023 verlaufen. Dies entspricht bei
Gaußverteilung in beiden Fällen dem 1/e²-Wert, die Angabe
ist dann beispielsweise dx,95
- über einen ausgewählten Leistungsanteil Pu
, der innerhalb der beiden linearen Grenzen hindurchtritt.
Der Anteil wird im Index mit u in Prozent genannt,
beispielsweise dx,50 für den Anteil 0,5
der Gesamtleistung.
- durch weitere Angaben wie den Ort des ersten Minimums
oder eines bestimmtes Maximums der Leistungsdichte in zwei
orthogonalen Richtungen mit minimaler und maximaler
Ausdehnung
2.5 Divergenz des Laserstrahls
Eine Eigenschaft aller Strahlenbündel - auch die von
Laserstrahlen - ist die, dass kein Strahlenbündel durch
einen einzigen Punkt laufen kann. Das ist gleichbedeutend
mit der Aussage, dass kein Laserstrahl ausschließlich aus
parallelen Strahlen (im Sinn der geometrischen Optik)
aufgebaut sein kann. Ein Laserstrahl kommt somit weder aus
einem Punkt, noch verläuft er in parallelen Grenzen. Die
Abweichung von der Parallelität wird Divergenz genannt. Zur
Beschreibung und Definition des Begriffes Divergenz von
Laserstrahlen sind weitere Informationen nötig. Diese werden
im nächsten Kapitel, 3 Strahlausbreitung, beschrieben.
Dort wird dann auch die Divergenz behandelt.
3 Strahlausbreitung
Ein Laserstrahl verläuft innerhalb einer Einhüllenden, der
Kaustik. Die Kaustik eines Bündels, deren Ursprung in einer
Quelle in einer Ebene liegt, ist ein einschaliger
Hyperboloid, im einfachsten Fall ein Rotationshyperboloid.
Ein Hyperboloid wird in jeder Ebene, die längs der
Strahlachse verläuft, über eine Hyperbel beschrieben, Bild
19. Im Hyperbelursprung liegt der engste Durchmesser d0.
Die engste Stelle des Laserstrahls wird Strahltaille
genannt.
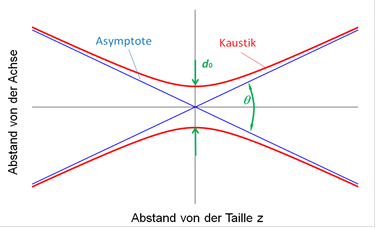 Bild 19: Kaustik eines
Laserstrahls (rot) mit Asymptoten (blau),
Bild 19: Kaustik eines
Laserstrahls (rot) mit Asymptoten (blau),
Taillendurchmesser d0 und
Divergenzwinkel θ
Liegt der Hyperbel-Ursprung im Ursprung des
Koordinatensystems und ist die Hyperbel normal ausgerichtet,
dann reichen zwei Parameter aus, um die Hyperbel eindeutig
zu bestimmen. Zur Beschreibung von Laserstrahlen bieten sich
deren Taillendurchmesser d0 und deren
Asymptotenwinkel θ als die beiden Parameter an. In
großem Abstand zum Ursprung der Hyperbel (der Strahltaille)
schmiegt sich die Hyperbel an die Asymptoten an. Der Strahldurchmesser nimmt dort proportional mit dem Abstand zu. Der Winkel zwischen den Asymptoten ist im Laserstrahl als "Divergenz θ" oder auch der "Divergenzwinkel θ"
definiert.
In großen Abständen zur Stahltaille sind Berechnungen über
die Asymptoten hinreichend genau. Die Gesetze der
Geometrischen Optik reichen aus. In der Nähe der
Strahltaille sind diese Gesetze nicht mehr gültig. Dort
führen Hyperbelgleichungen zu korrekten Ergebnissen von
Berechnungen. Die Gleichung einer Hyperbel mit den
Strahlparametern d0 und θ in
Ursprungsdarstellung ist:
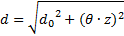 (26)
(26)
wobei z der Abstand vom Koordinatenursprung ist.
Der Strahl läuft in positive z-Richtung. Abstände
zum Ursprung werden dann als groß bezeichnet, wenn in der
Hyperbelgleichung d0 gegenüber 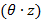 vernachlässigt
werden kann,
vernachlässigt
werden kann,  . Dann ist
. Dann ist 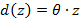 .
Der Strahldurchmesser nimmt dort proportional zum Abstand
zu.
.
Der Strahldurchmesser nimmt dort proportional zum Abstand
zu.
Die Divergenz θ , also die Änderung der
Strahldurchmesser im Strahlverlauf, ist mit der gewählten Definition
des Durchmessers verbunden! [15] Wenn die
Strahlbegrenzung beispielsweise auf den Wendepunkt der
Leistungsdichte bezogen wird, dann sind beide Größen d
und θ halb so groß wie im 1/e2 -
Bezug, Tabelle 1.
Mit den Parametern d0 und θ ist
die Ausbreitung eines Laserstrahls eindeutig festgelegt. Für
weitere Betrachtungen sind zwei weitere Größen hilfreich:
die Rayleighlänge zR und die
Strahlinvariante KI.
Die Rayleighlänge lässt sich über die Strahlparameter d0
und θ definieren:
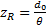 (27)
(27)
Sie ist (wie aus der Hyperbelgleichung ableitbar) der
Abstand von der Stahltaille, in dem der Strahldurchmesser
den Betrag 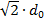 annimmt. Die Rayleighlänge gibt
somit Auskunft darüber, wie "schlank" der Laserstrahl ist.
annimmt. Die Rayleighlänge gibt
somit Auskunft darüber, wie "schlank" der Laserstrahl ist.
Die zweite Größe, die Strahlinvariante, ist
definiert als
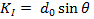 (28)
(28)
oder für kleine θ
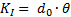 (29)
(29)
Die Schreibweise für kleine Winkel entspricht der in der
Geometrischen Optik bekannten „Helmholtz-Lagrange-Invarianten„ [16],
die für parachsiale Abbildungen gefunden wurde. Sie ist
prinzipiell für jede fehlerfreie Abbildung eines Objekts
gültig. [17] und soll im Folgenden auch kurz hergeleitet werden, Bild 20.
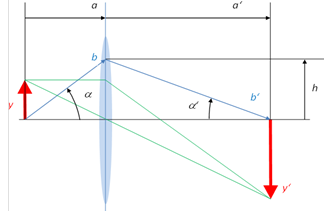 Bild 20: Zur
Helmholtz-Lagrange-Invarianten
Bild 20: Zur
Helmholtz-Lagrange-Invarianten
In diesem Modell wird die Optik für eine fehlerfreie
Abbildung durch eine dünne Linse symbolisiert.
Das Objekt mit der Objekthöhe y befindet sich in
der Objekteben. Sein Bild in der Bildebene hat die
Bildhöhe y'. Der Abbildungsmaßstab β'
ist definiert als
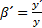 (30)
(30)
Der Strahlensatz sagt aus
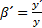 (31)
(31)
weiter gilt
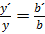 (32)
(32)
denn bei fehlerfreier Abbildung konvergieren alle Strahlen
aus einem Objektpunkt in den entsprechenden Bildpunkt und
durchlaufen gleiche optische Weglängen. Damit ist für diese
verschiedenen Wege der Abbildungsmaßstab der Gleiche.
Zusätzlich gilt: 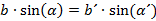
und mit Gleichung (32) die Beziehung
y ⋅ sin(α) = y´ ⋅ sin(α´)
= konstant(33)
Für kleine Winkel (im Parachsialbereich der Geometrischen
Optik) gilt sin(α) = α. Damit führt Gleichung (32)
zur Helmhotz-Lagrange-Invarianten, Gleichung (34):
y ⋅ α = y´ ⋅ α´
(34)
Dies bedeutet, dass sich bei beliebigen korrekten
Abbildungen das Produkt zwischen den Objekthöhen mit
den dazugehörenden halben &ooml;ffnungswinkeln nicht ändert.
Übertragen auf die Größen eines Laserstrahls mit dem
Taillendurchmesser d0 und der Divergenz θ
bedeutet dies auch, dass deren Produkt d0
⋅ sin( θ ) (oder bei kleinen Winkeln d0
⋅ θ ) invariant gegen Abbildungen ist. Dieses
Produkt wird deshalb wie in Gleichung (28) und Gleichung
(29) definiert, Strahlinvariante oder Strahlparameterprodukt [18]
genannt.
Die Strahlinvariante, verknüpft mit der Heisenbergschen
Unschärfe-Relation, führt zu einer Grenze, die für Strahlung
jeder Art gilt. Da eine Kenntnis dieser Grenze hilfreich für
verschiedene Betrachtungen von Laserstrahlen ist, folgt eine
ausführlichere Ableitung dieser Grenze.
3.1 Auswirkung der Heisenbergschen Unschärferelation
Laserstrahlen sind räumlich begrenzte elektromagnetische
Wellen oder ein räumlich begrenzter Strom von Photonen. Die
einzelnen Photonen führen neben der Energie einen Impuls
mit. Die Unschärferelation bezieht sich auf den
Photonenstrom und auf die Wirkung [19]. Sie
wurde von Heisenberg aus quantenmechanischen Betrachtungen
mit dem Planckschen Wirkungsquantum h gefunden. Das
Plancksche Wirkungsquantum ist neben der
Lichtgeschwindigkeit und der Gravitationskonstanten die
dritte Naturkonstante. Die Unschärferelation besagt in einem
Fall, dass Position und Impuls eines Teilchens nicht
gleichzeitig genaue Beträge einnehmen. Bei bekannter
Position des Photons ist dessen Impuls unsicher und
umgekehrt. Die Unschärfe des Ortes 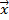 und des Impulses
und des Impulses 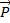 werden jeweils durch
deren statistische Streuung
werden jeweils durch
deren statistische Streuung 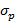 und
und 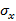 definiert
definiert
Angewandt auf den Laserstrahl der Wellenlänge λ und
damit mit der Frequenz ν, wird hier die Ebene der
Strahltaille betrachtet. Der Strahl tritt senkrecht durch
diese Ebene innerhalb seines Durchmessers hindurch.
Quantenmechanisch wird seiner Frequenz ν eine
Energie E zugeordnet (E = h⋅ν). Diese
Energie kann in Laserstrahlen sehr scharf begrenzt sein
(Kapitel 2.1.4 und 2.1.5), wie Heisenbergs Energie-Zeit-Unschärferelation zeigt. Daraus folgt, dass der Betrag des
mitgeführten Impulses 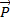 ebenso scharf
begrenzt ist; denn
ebenso scharf
begrenzt ist; denn 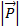 und E
eines Photons sind über die Lichtgeschwindigkeit c
verknüpft:
und E
eines Photons sind über die Lichtgeschwindigkeit c
verknüpft: 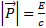 . Eine
Unschärfe des Impulses kann somit nur in einer Unschärfe der
Richtung des Impulsvektors liegen, also in
Winkelabweichungen von der Strahl-Ausbreitungsrichtung. Dies
wird im Folgenden für den Laserstrahl in der Ebene (am Ort)
seiner engsten Begrenzung betrachtet.
. Eine
Unschärfe des Impulses kann somit nur in einer Unschärfe der
Richtung des Impulsvektors liegen, also in
Winkelabweichungen von der Strahl-Ausbreitungsrichtung. Dies
wird im Folgenden für den Laserstrahl in der Ebene (am Ort)
seiner engsten Begrenzung betrachtet.
Die engste Begrenzung ist die Strahltaille mit dem
Durchmesser d0. Dort werden die gesuchten
Beziehungen für Impuls 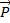 und Ort
und Ort 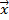 abgeleitet. In dem
Modell beziehen sich Radius r und Winkel α
auf die Standardabweichung σ, also auf die
Wendepunkte der Gaußschen Glockenkurven, welche die
Wahrscheinlichkeit des Photonenstroms entsprechend der
Wellenlänge λ bezüglich Ort und Impuls beschreiben;
denn die Wahrscheinlichkeitsrechnung bezieht sich auf
Standardabweichungen von eindimensionalen
Normalverteilungen. In einem zweiten Schritt werden die
Aussagen für die Wendepunkte σp und σx
in Aussagen für die Stahlparameter d0 und
θ transformiert.
abgeleitet. In dem
Modell beziehen sich Radius r und Winkel α
auf die Standardabweichung σ, also auf die
Wendepunkte der Gaußschen Glockenkurven, welche die
Wahrscheinlichkeit des Photonenstroms entsprechend der
Wellenlänge λ bezüglich Ort und Impuls beschreiben;
denn die Wahrscheinlichkeitsrechnung bezieht sich auf
Standardabweichungen von eindimensionalen
Normalverteilungen. In einem zweiten Schritt werden die
Aussagen für die Wendepunkte σp und σx
in Aussagen für die Stahlparameter d0 und
θ transformiert.
Nach Heisenberg kann das Produkt aus Impulsunsicherheit 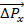 mit der
Ortsunsicherheit
mit der
Ortsunsicherheit 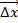 in derselben Ebene
einen bestimmten Betrag nicht unterschreiten. Für
normalverteilte Impuls- und Ortswahrscheinlichkeiten und
deren Standardabweichungen
in derselben Ebene
einen bestimmten Betrag nicht unterschreiten. Für
normalverteilte Impuls- und Ortswahrscheinlichkeiten und
deren Standardabweichungen 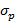 und
und 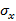 ist diese:
ist diese:
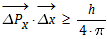 (Heisenbergsche
Unschärferelation) (35).
(Heisenbergsche
Unschärferelation) (35).
Weiter gilt die Teilchen-Welle-Äquivalenz nach de Broglie:
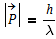 (36).
(36).
Für einen Laserstrahl der Wellenlänge λ , dessen
engste Begrenzung in der Strahltaille mit dem Durchmesser d0
liegt, lassen sich Impuls 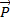 und Ort
und Ort
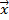 wie folgt betrachten, Bild 21, und daraus die gesuchten
Beziehungen ableiten.
wie folgt betrachten, Bild 21, und daraus die gesuchten
Beziehungen ableiten.
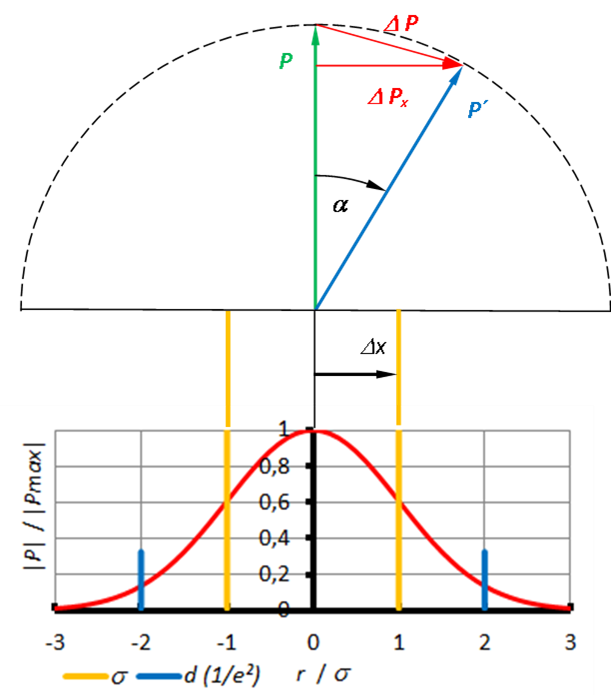 Bild 21: Anwendung der
Unschärferelation von Heisenberg auf den Laserstrahl.
Betrachtet wird die Ebenen der Strahltaille, das ist die
Position im Strahl mit dem engsten Durchmesser. Die
Leistungsdichte und damit die Dichte des Photonenstroms
ist gaußverteilt.
Bild 21: Anwendung der
Unschärferelation von Heisenberg auf den Laserstrahl.
Betrachtet wird die Ebenen der Strahltaille, das ist die
Position im Strahl mit dem engsten Durchmesser. Die
Leistungsdichte und damit die Dichte des Photonenstroms
ist gaußverteilt.
Die Photonen in der Strahlachse weisen den Impuls 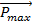 auf. Betrachtet wird
die Unsicherheit in der Strahltaille in Richtung der
Ortsunsicherheit, also in x-Richtung. Die Unsicherheiten beziehen sich auf die Wendepunkte der Gaußschen Glockenkurve.
auf. Betrachtet wird
die Unsicherheit in der Strahltaille in Richtung der
Ortsunsicherheit, also in x-Richtung. Die Unsicherheiten beziehen sich auf die Wendepunkte der Gaußschen Glockenkurve.
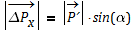 (aus der Geometrie)
(aus der Geometrie)
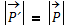 (da feste Wellenlänge); somit gilt:
(da feste Wellenlänge); somit gilt:
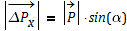
multipiziert mit der Ortsunsicherheit:
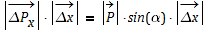
mit de Broglie:
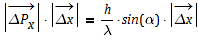
Mit der Unschärfe-Relation gilt:
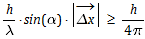 woraus folgt:
woraus folgt:
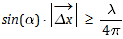
Diese Aussage gilt für den Halbwinkel α und für
den Radius r (Abstand von der Strahlachse in x
Richtung) jeweils für die Wendepunkte der Normalverteilung.
Der Wechsel auf den 1/e² Bezug für Radius 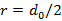 und Winkel
und Winkel 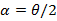 erfolgt mit
dem Faktor 4, siehe Bild 14 und Tabelle 1. Damit führt die
Unschärferelation zu der Aussage
erfolgt mit
dem Faktor 4, siehe Bild 14 und Tabelle 1. Damit führt die
Unschärferelation zu der Aussage
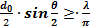 (37)
(37)
Das entspricht dem Strahlparameter-Produkt. Für kleine
Divergenzen θ bedeutet dies, dass das
Strahlparameter-Produkt K = (d0 /
2) ⋅ (θ / 2) nicht kleiner sein kann als λ / π.
Der nächste Übergang vom Radius und Halbwinkel zu
Durchmesser d0 und Divergenz θ
erfolgt wieder mit einem Faktor 4. Hiermit wird die
Strahl-Invariante erfasst.
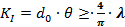 (38)
(38)
Die Stahlinvarinate KI kann also nich
kleiner sein als etwa die Wellenlänge.
Diese theoretische Untergrenze wird in Gaußstrahlen
erreicht. Ein solcher Gaußstrahl wird Grundmodelaserstrahl
genannt. Andere Gaußstrahlen haben eine größere Invariante;
denn die Heisenbergsche Unschärfe-Relation enthält die
Relation "≥". Das "größer als" wird mit einem Faktor, dem
Vergrößerungsfaktor M 2 gekennzeichnet. Damit ist
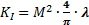 (39)
(39)
Dieser "Vergrößerungsfaktor" als Bestandteil der
Invarianten KI gibt somit an, wie weit
der gegebene Laserstrahl von der naturgegebenen Untergrenze
"Unschärferelation" abweicht.
3.2 Strahltransformation
Die Kaustik eines Laserstrahls lässt sich über optische
Komponenten in eine andere transformieren. Eine
Transformation erfolgt entsprechend bekannter physikalischer
Gesetze. Einfache Gesetze sind aus der GEOMETRISCHEN OPTIK [20]
bekannt, so die (Brennpunkt-bezogene) Newtonsche
Abbildungsgleichung. Über diese lässt sich berechnen, wie
ein Objekt mit dem Abstand z zum ersten Brennpunkt
einer Fokussieroptik der Brennweite f abgebildet
wird. Die Newtonschen Abbildungsgleichungen für die
Bildgröße und für die Bildlage beziehen sich auf die
Brennebenen. Hierdurch werden die Gleichungen im Vergleich
zur konventionellen (Hauptebenen-bezogenen) übersichtlicher.
Für beidseitig der Abbildungsoptik gleiche Brechungsindices
führt der Strahlensatz, Bild 22, zu
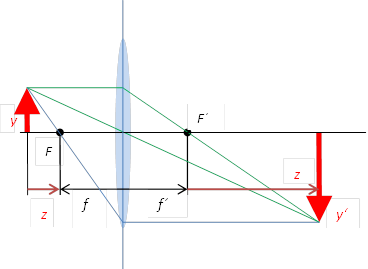 Bild 22: Zur
Newtonschen Abbildungsgleichung
Bild 22: Zur
Newtonschen Abbildungsgleichung
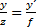 (40)
(40)
sowie zu 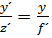
damit gilt
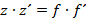
weiter ist 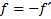
somit gilt auch
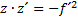 (41)
(41)
Gleichung (40) wird zur Ableitung der Gesetze für die
Transformation der Strahltaille benötigt,
Gleichung (41) für die zur Transformation der
Strahltaillenlage (Fokusverschiebung).
3.2.1 Transformation des Taillendurchmessers
Für die Beschreibung der optischen Transformation eines
Laserstrahls wird die Strahltaille als Objekt betrachtet.
Die Strahltaille lässt sich mit optischen Komponenten nach
Gesetzen der Geometrischen Optik transformieren. Gleichung
(39) führt zu einer Transformation des Objektes
"Taillendurchmessers d0 " in sein Bild,
"Taillendurchmesser d0´ " wenn die Größen y
und y´ ersetzt werden durch d0
und d0´. Damit wird Gleichung (40) zu
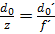 (42)
(42)
Die Strahltaille mit dem Durchmesser d0
wird transformiert in den Fokusdurchmesser d0´
über die Gleichung
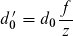 (43)
(43)
Dies wäre der berechnete Durchmesser des
Strahltaillenbildes, wenn die Unschärferelation nicht
berücksichtigt werden müsste, Bild 23 roter Graph. Die
Abbildungsgleichung (43) ist für z = 0 nicht
definiert. Der Graph zeigt dort eine Polstelle, die bei
Transformation von Laserstrahlen nicht beobachtet wird. Also
gelten die Gesetze der Geometrischen Optik mit Sicherheit nicht in der Nähe von z = 0.
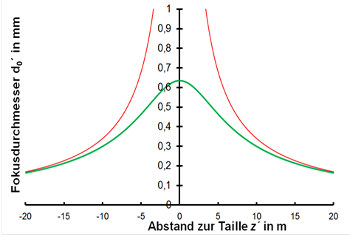 Bild
23: Durchmessertransformation durch Abbildung eines
Laserstrahls für
verschiedene Abständen z des Optikbrennpunktes von der Strahl-taille.
Bild
23: Durchmessertransformation durch Abbildung eines
Laserstrahls für
verschiedene Abständen z des Optikbrennpunktes von der Strahl-taille.
d0 = 17 mm, f = 200 mm, KI = 54 µm rad, mit Berücksichtigung der Beugung (grün)
und nach Newton (rot), der Abstand z ist
Brennpunkt-bezogen
Die Unschärfe ist also nicht zu vernachlässigen, wenn Größen eines Strahls (oder auch eines anderen abzubildenden Objektes) in der Nähe eines Brennpunktes des Abbildungssystems betrachtet werden.
Das liegt daran, dass die Gesetze der Geometrischen Optik auf homozentrischen Bündeln beruhen, also für Strahlen gelten, die von einem Punkt ausgehen und über Abbildungsoptiken mit Brennpunkten in einen Punkt transformiert werden. Aufgrund der Unschärferelation ist dies für physikalische Strahlung nicht möglich, siehe 3.1. Diese Strahlenbündel verlaufen innerhalb von Hyperboloiden und nicht innerhalb von Kegeln. Die Unterschiede zwischen Kegel und Hyperboloiden können sich in Berechnungen von Abbildungsergebnissen für Bereiche auswirken, in denen sich beide Figuren merkbar unterscheiden. Das ist gerade der Bereich um die Stahltaillen. Die Ergebnisse sind dann falsch, wenn dort ein Brennpunkt der Optik des Abbildungssystems positioniert ist.
Bei Berücksichtigung der Unschärfe (zur Ermittlung des korrekten Ergebnisses) wird die Abbildungsgleichung, Gleichung (42), durch einen Term modifiziert, welcher die Hyperboloid-Form der Kaustik berücksichtigt: Dieser Term ist die Rayleighlänge, Gleichung (27).
[21]
Damit ist Gleichung (44) die korrekte Abbildungsgleichung für Gaußstrahlen.
Die Rayleighlänge enthält zwei Parameter d0 und θ, welche die Hyperbel eindeutig beschreiben. Damit sind zwei weitere Schreibweisen gleichbedeutend, Gleichung (44): Gleichung (45) und Gleichung (46).
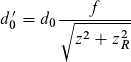 (44)
(44)
oder
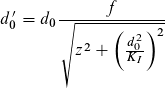 (45)
(45)
oder
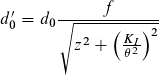 (46)
(46)
In Berechnungen über die korrekte Abbildungsgleichung, Bild 23, grüner Graph, tritt eine Polstelle nicht auf. Das Ergebnis zeigt dort, wo die Geometrische Optik eine Polstelle anzeigt, einen endlichen Bilddurchmessers (Fokusdurchmessers) auf. Die Position der primären Strahltaille ist dabei der primäre (objektseitige)
Brennpunkt der Abbildungsoptik, das heißt, bei z = 0.
In großen Abständen der primären Strahltaille zum
Optikbrennpunkt kann die Rayleighlänge vernachlässigt
werden. Das korrekte Ergebnis wird dann durch die
Berechnungen über die Geometrische Optik angenähert. Die
einfachen Gesetze aus der Strahlenoptik gelten wieder
näherungsweise.
Das Maximum des Bilddurchmessers (der maximale
Fokusdurchmesser) lässt sich berechnen, wenn die Kaustik des
Ausgangsstrahls bekannt ist, das heißt, wenn zwei
Strahlparameter bekannt sind, welche die Strahlkaustik
eindeutig kennzeichnen. Für z = 0 führt Gleichung
(43) mit zR = d0 /
θ zum Ergebnis
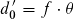 (47)
(47)
Für die Praxis gilt damit näherungsweise, dass der
Fokusdurchmesser (Bilddurchmesser) hinter einer
Fokussieroptik als Produkt von Brennweite mal Divergenz
abgeschätzt werden kann; denn die Fokussieroptik befindet
sich in vielen Fällen in der Nähe des Lasers und damit in
der Nähe der primären Strahltaille.
Der Abbildungsmaßstab ist definiert als ß' = y' / y,
siehe Gleichung (30). Das gilt auch für die
Durchmessertransformation von Strahltaillen. Die Gesetze der
Geometrischen Optik, hier Gleichung (42), würden zum
Ergebnis führen
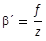 (48)
(48)
Das Ergebnis gilt wiederum nur in großen Abständen der Transformationsoptik von der Strahltaille, wie die Diskussion zu Bild (23) zeigt. Der korrekte Abbildungs-Maßstab ergibt sich aus der korrekten Abbildungsgleichung, Gleichung (43). Der Maßstab ist somit
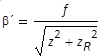 (49)
(49)
3.2.2 Transformation der Strahltaillenlage
Zur Beschreibung der Position der Strahltaille nach einer
Abbildung über eine optische Komponente werden wieder
Gesetze aus der Geometrischen Optik hinzugezogen.
Ausgegangen wird von der Abbildungsgleichung nach der
Newtonschen Formulierung Gleichung (40) mit Bild 22.
Der Bildort der Strahltaille liegt im Abstand z' zum
zweiten Brennpunkt der Optik.
Die explizite Form aus der
geometrischen Optik für z' ist
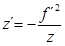 (50)
(50)
Diese Abbildungsgleichung gilt jedoch nicht mehr, wenn die
Unschärfe berücksichtigt werden muss
[22], das heißt, wenn sich
die abbildende Optik in der Nähe der Strahltaille befindet.
Für diesen Fall wird die Newtonsche Abbildungsgleichung
durch einen Unschärfeterm zR modifiziert,
Bild 24 und Gleichung (59) zu:
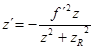 (51)
(51)
Mit 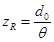 und
und 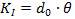 sind
entsprechende Modifikationen für weitere bevorzugte
Strahlparameter möglich und üblich, siehe Tabelle 2. Über diese Gleichungen wird der Bereich um die Strahltaille korrekt wiedergegeben, Bild 24, grüner
Graph.
sind
entsprechende Modifikationen für weitere bevorzugte
Strahlparameter möglich und üblich, siehe Tabelle 2. Über diese Gleichungen wird der Bereich um die Strahltaille korrekt wiedergegeben, Bild 24, grüner
Graph.
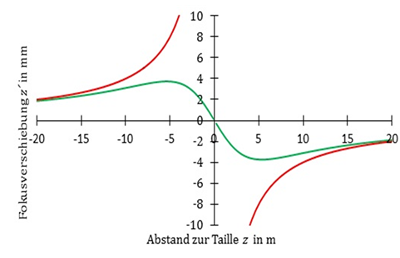 Bild
24: Transformation der Taillenlage
(Fokusverschiebung) durch Abbildung eines
Laserstrahls für verschiedene Abstände z des
Optikbrennpunktes von der Strahltaille
d0 = 17 mm, f = 200 mm, K I = 54 µm rad, mit Berücksichtigung der Beugung (grün)
und nach Newton (rot), der Abstand z ist
Brennpunkt-bezogen
Bild
24: Transformation der Taillenlage
(Fokusverschiebung) durch Abbildung eines
Laserstrahls für verschiedene Abstände z des
Optikbrennpunktes von der Strahltaille
d0 = 17 mm, f = 200 mm, K I = 54 µm rad, mit Berücksichtigung der Beugung (grün)
und nach Newton (rot), der Abstand z ist
Brennpunkt-bezogen
Für die Berechnung wurde die Modifizierung der Gleichung (51)
gewählt, in der die Rayleiglänge durch die üblicherweise bekannten Größen d0 und θ
des Primärstrahls ersetzt wurde, siehe Tabelle 2. Die Strahlparameter entsprechen denen eines CO2-Hochleistungslasers.
Näherungslösungen über Gesetze, die aus dem Bereich der Geometrischen Optik bekannt sind, gelten für größere Abstände zur Strahltaille hinreichend genau. Das ist der Fall, wenn die Abstände der Strahltaille zum primären Brennpunkt der Abbildungsoptik groß gegenüber der Rayleighlänge sind, also für den Fall z >> zR. Das zeigt Gleichung (50). Bemerkenswert ist, dass dann, wenn die primäre Strahltaille im primären Fokus der Abbildungsoptik liegt (z = 0), die sekundäre Strahltaille (der Fokus) in den sekundären Brennpunkt abgebildet wird; denn zR≠ 0.
3.2.2.1 Position der Extrema
Die Fokusverschiebung, Bild 24, weist zwei Extremwerte
auf. Die Lage z'extr dieser Extrema lässt
sich über das bekannte Verfahren zur Extremwertbestimmung
aus der Abbildungsgleichung, Gleichung (51) wie folgt
ermitteln:
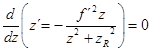 Diese Ableitung
nach z ergibt:
Diese Ableitung
nach z ergibt:
und somit liegt das Maximum bei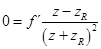
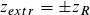 dies ist
gleichbedeutend mit:
dies ist
gleichbedeutend mit:
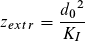 denn
zR = d0 / θ
und θ = KI / d0
denn
zR = d0 / θ
und θ = KI / d0
Der Fokus ist also gegenüber dem sekundären Brennpunkt der
Optik maximal verschoben, wenn der primäre Brennpunkt im
Abstand der Rayleighlänge von der Strahltaille entfernt ist.
Mit Kenntnis der Lage der Extrema 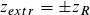 ist auch die
maximale Fokusverschiebung eindeutig festgelegt, und zwar
über die Abbildungsgleichung, Gleichung (51):
ist auch die
maximale Fokusverschiebung eindeutig festgelegt, und zwar
über die Abbildungsgleichung, Gleichung (51):
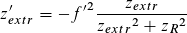 Hier ist zR
die Rayleighlänge des Primärstrahls!
Hier ist zR
die Rayleighlänge des Primärstrahls!
Damit verschiebt sich der Fokus maximal um
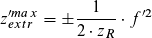 dies ist
gleichbedeutend mit
dies ist
gleichbedeutend mit
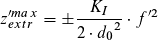 denn zR = d0 / θ
und θ = KI / d0
denn zR = d0 / θ
und θ = KI / d0
3.2.3 Folgerung aus den Diskussionen:
Wenn ein Laserstrahl vorgegebener Qualität (gekennzeichnet durch die Strahl-Invariante KI) in verschiedenen Positionen entlang des Strahlweges über eine Optik mit festgelegter Brennweite fokussiert werden soll und dabei möglichst geringe Unterschiede in der Fokusplage gewünscht sind, dann kann dies durch Aufweiten des Primärstrahls erreicht werden. Eine Vergrößerung des Taillendurchmessers im Primärstrahl über einen Faktor x verringert die maximale Fokusverschiebung quadratisch um den Faktor (1 / x)2. Den entsprechenden quadratischen Einfluss hat der Taillendurchmesser auf die Positionen der Fokussieroptik im Primärstrahl, die zu den extremalen Fokusverschiebungen führen: Mit Aufweitung des Taillendurchmessers um den Faktor x verschiebt sich die Rayleighlänge des Primärstrahles, also die Positionen der Fokussieroptik, in denen sich der Fokus maximal verschiebt, um den Faktor x2.
3.3 Einige Formeln zur Beschreibung von Eigenschaften
eines Laserstrahls
Tabelle 2: Formelsammlung zur Beschreibung von
Laserstrahlen
|
E0
|
Leistungsdichte im Zentrum des Grundmodestrahls
|
|
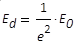
|
Zur Durchmesser-Definition: Leistungsdichte am Ort
des Strahldurchmessers d im
rotations-symmetrischen Strahl mit Gaußverteilung
der Leistungsdichte (Grundmode, Maximum E0)
|
|
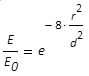
|
Verteilung der Leistungsdichte in einem
rotationssymmetrischen Grundmodestrahl, Durchmesser
d, Maximum E0, Radius r
|
|
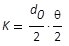
|
Strahlparameterprodukt (SPP)
|
|
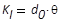
|
Strahl-Invariante
|
|
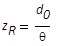
|
Rayleigh-Länge
|
|
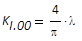
|
Strahl-Invariante für den Grundmode
|
|
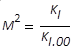
|
Beugungsmaßzahl M2
|
|
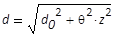
|
Gleichung der Kaustik
|
|
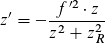
|
Transformation der Strahltaillenposition
(Fokusposition) mit Brennweite f,
bekannt ist die Rayleigh-Länge,
zu
beachten: f = - f '
|
|
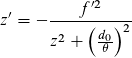
|
Transformation der Strahltaillenposition
(Fokusposition) mit Brennweite f,
bekannt sind d0 und θ,
zu
beachten: f = - f '
|
|
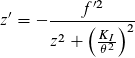
|
Transformation der Strahltaillenposition
(Fokusposition) mit Brennweite f,
bekannt sind KI und θ,
zu
beachten: f = - f '
|
|
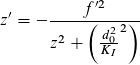
|
Transformation der Strahltaillenposition
(Fokusposition) mit Brennweite f,
bekannt sind d0 und KI,
zu
beachten: f = - f '
|
|
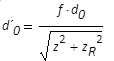
|
Transformation des Taillendurchmessers d0
in den sekundären Durchmesser
(Fokus-durchmesser) d'0 mit
Brennweite f ; Abstand z des
primären Fokus von primärer Strahltaille;
Rayleigh-Länge zR
|
|
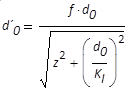
|
Transformation des Taillendurchmessers d0
in den sekundären Durchmesser (Fokus-durchmesser) d'0
mit Brennweite f ; Abstand z des
primären Fokus von primärer Strahltaille; Invariante
KI,
|
|
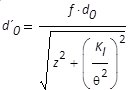
|
Transformation des Taillendurchmessers d0
in den sekundären Durchmesser (Fokus-durchmesser) d'0
mit Brennweite f ; Abstand z des
primären Fokus von primärer Strahltaille; Invariante
KI; primäre Divergenz θ
|
|
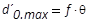
|
Taillendurchmesser nach Fokussierung über die
Brennweite f bei einer Divergenz θ
des Primären Strahls. Die primäre Strahltaille liegt
im primären Brennpunkt. Der Durchmesser ist in
dieser Position maximal.
|
|
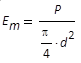
|
Mittlere Leistungsdichte in einem
rotations-symmetrischen Grundmodestrahl (bezogen auf
den Querschnitt innerhalb des Durchmessers)
|
|
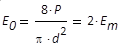
|
Maximum der Leistungsdichte in einem
rotationssymmetrischen Grundmodestrahl; dies liegt
im Zentrum
|
|
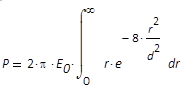
|
Gesamtleistung eines rotationssymmetrischen
Grundmodestrahls mit Durchmesser d und der
Leistungsdichte E0 im Maximum
(Zentrum)
|
|
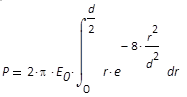
|
Leistungsfluss innerhalb des Durchmessers d in
einem rotationssymmetrischen Grundmode-strahl mit
Durchmesser d und der Leistungsdichte E0
im Maximum (Zentrum)
|
|
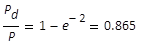
|
Leistungsanteil innerhalb des Durchmessers d
in einem rotationssymmetrischen Grundmode-strahl,
bezogen auf die Gesamtleistung
|
|
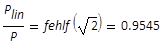
|
Leistungsanteil innerhalb zweier linearer
Begrenzungen in der Position d in einem
rotationssymmetrischen Grundmodestrahl, bezogen auf
die Gesamtleistung
|
|
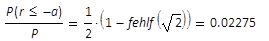
|
Leistungsanteil außerhalb des Durchmessers im
Grundmodestrahl mit rotationssym-metrischem
Querschnitt, der durch eine lineare Blende in der
Begrenzung d ausgeblendet wird
|
|
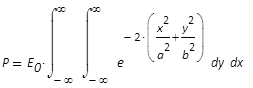
|
Gesamtleistung in einem Grundmodestrahl bei
elliptischem Querschnitt mit den Ellipsenparametern
a und b, sowie der maximalen
Leistungsdichte (im Zentrum) E0
|
|
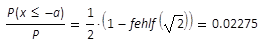
|
Leistungsanteil außerhalb des Ortes einer
Strahlabmessung im Grundmodestrahl mit elliptischem
Querschnitt, ausgeblendeter durch eine lineare
Blende
|
4 Zusammenfassung
Ausgang der theoretischen Behandlung von Laserstrahlen - so
wie sie für die Materialbearbeitung in industrieller
Anwendung verwendet werden - ist der Hintergrund, dass auch
Laserstrahlen nichts anderes sind als Licht im allgemeinsten
Sinn. Das bedeutet, dass in vielen Fällen Kenntnisse der
allgemeinen optischen Gesetze ausreichen, um das Verhalten
von laserstrahlen zu verstehen und zu beschreiben. Die
Gesetze der "Geometrischen Optik" versagen lediglich in
Brennpunktbereichen.
Auf dieser Basis wurden in den vorangegangenen Kapiteln
die wesentlichen Eigenschaften von Laserstrahlen
dargestellt, beschrieben und auch abgeleitet, die in der
industriellen Materialbearbeitung eingesetzt werden. Damit
sollte der Leser in der Lage sein,
- Eigenschaften von Laserstrahlen zu verstehen und zu
beurteilen,
- Laserstrahlen für gewünschte Anwendungen auszuwählen,
- Laserstrahlen an die Anforderungen der gewünschten
Anwendung anzupassen,
- Eigenschaften von Laserstrahlen zu messen.
Die Zusammenstellung der Formeln hilft zudem,
Beschreibungen von Laserstrahlen zu verstehen, die in der
industriellen Materialbearbeitung verwendet werden.
Referenzen
[1] Hier wird
der Begriff aus der Geometrischen Optik gewählt, um zu
kennzeichnen, dass mit „Strahl“ nicht der
mathematische Begriff gemeint ist, und um auf seine
räumliche Ausdehnung hinzuweisen
[2] Hier
betrachtet im Wellenbild
[3] Welle,
vereinfacht nach DIN 1311: zeitlich periodische
Änderung eines Zustandes im Raum, die sich einsinnig
räumlich ändert
[4] Über die
räumliche Kohärenz werden beispielsweise
Sterndurchmesser gemessen.
[5]
Ausführlich behandelt werden Laser im Lehrbuch „Bert
Struve: Einführung in die Lasertechnik;
VDE-Verlag,
Berlin 2009“
[6]
Beschrieben im Kapitel 2.1.1 Transversale Modenordnung
[7]
Beschrieben im Kapitel 3 Strahlausbreitung
[8]
Beschrieben im Kapitel 3.1 Auswirkung der Heisenbergschen Unschärferelation
[9] Kapitel
1 Grundlegende Definitionen
[10]
Beschrieben im Kapitel 3.2 Strahltransformation
[11]
Laserstrahl-Modenordnungen werden behandelt in Kapitel
2.1 Gaußstrahlen
[12] Beschrieben im Kapitel 3.1 Auswirkung der Heisenbergschen Unschärferelation
[14] Moden
werden beschrieben im Kapitel 2.1.1
[15]
Beschrieben in Kapitel 2.3
[16] In dieser
Form für beidseitig der Optik gleiche
Brechungsindices, Lehrbuch Gottfried Schröder,
Hanskarl Treiber: Technische Optik, Vogel Fachbuch
2002; S. 33
[17] Hier sei
darauf hingewiesen, dass strahlenoptisch wirkende
Systeme wie Linsen- oder Spiegeloptiken keine
dreidimensional ausgedehnten Objekte maßstabsgetreu
abbilden können. Das ist nur über wellenoptische
Methoden (Holographie) möglich.
[18] In DIN ist
das Strahlparameterprodukt ein Viertel der hier
festgelegten Definition
[19] Die Wirkung
S ist eine physikalische Größe mit der
Dimension Energie mal Zeit oder Impuls mal Weglänge.
[20] Lehrbuch
Gottfried Schröder, Hanskarl Treiber: Technische
Optik, Vogel Fachbuch 2002
[21] Aus wellenoptischen Betrachtungen abgeleitet zum Beispiel in: J. Eichler; H.-J. Eichler: Laser, Grundlagen-Systeme-Anwendungen; Springer-Verlag Berlin …, 1991
[22] Aus wellenoptischen Betrachtungen abgeleitet zum Beispiel in: J. Eichler; H.-J. Eichler: Laser, Grundlagen-Systeme-Anwendungen; Springer-Verlag Berlin, …, 1991
