Trennen
Der einleitende Vorspann zum Thema "Trennen" verfolgt zwei Ziele. Zum ersten werden die Begriffe definiert, die im Ingenieurwesen üblich sind, um damit schneller und sicher in die Thematik einzusteigen. Zum zweiten werden die Normen zu den Fertigungsverfahren aufgeführt, die sich auf den Themenbereich beziehen. Diese sind auch in DIN-Taschenbüchern zusammengefasst erhältlich, so dass ein Aufsuchen dieser Normen auch Alternativen zu den lasertechnischen Bearbeitungsmöglichkeiten gesehen werden.[1]
"Trennen" beschreibt die Technik, über welche die Form eines Körpers durch örtliches Aufheben des Zusammenhaltes geändert wird. Die Endform ist dabei schon im Ausgangskörper enthalten. Diese Definition bezieht sich auf Fertigungsverfahren (DIN 8590). Sie wird hier für die Bearbeitung von Stoffen allgemein gewählt.
Die verschiedenen Möglichkeiten des Trennens (DIN 8590 Hauptgruppe 3) werden systematisch weiter gegliedert. Für die Bearbeitung mit Laserstrahlen sind die Gruppen 3.1 Zerteilen und die Gruppe 3.4 Abtragen von Interesse.
In die Gruppe 3.1 "Zerteilen" fällt das Spalten. Eingegangen wird hierauf in diesem Kapitel unter der Übeschrift Trennen durch Thermoschock. Die Gruppe 3.4 "Abtragen" enthält die Untergruppe 3.4.1 Thermisches Abtragen und 3.4.2 "Chemisches Abtragen". In der lasertechnichen Materialbearbeitung beruht das "Chemische Abtragen" auf der direkten Wirkung der Photonen auf die Grundbausteine "Moleküle" der Stoffe. Über geeignete Photonenenergien werden hierbei Molkülverbindungen wärmearm gelöst
Das "Thermische Abtragen", Untergruppe 3.4.1, enthält unter Nummer 3.4.1.5 das lasertechnisch genutzte "Thermische Abtragen durch Strahl". Dies ist zusätzlich in DIN 2310 Teil 6 erfasst. Dort sind die Thermischen Schneidverfahren beschrieben, welche weiter eingeteilt werden nach
- der Physik des Schneidvorgangs
- der Art der Fertigung
- dem Energieträger
Die Physik des Schneidvorganges umfasst zwei Hauptvorgänge
Die Bezeichnung des Verfahrens bezieht sich auf die Fugenbildung, also auf das Entstehen der Schnittfuge. Dies kann Brennen (Oxidieren), Schmelzen oder Dampfbildung sein. Gewählt wird der Begriff, der den überwiegenden Anteil am Prozess der Fugenbildung kennzeichnet; denn alle praktisch angewendeten Verfahren sind Mischformen dieser drei Vorgänge. So ist über jeder Schmelze auch Dampf vorhanden, sogar über jedem Feststoff bei Raumtemperatur.
Mit dem Energieträger Laserstrahl werden somit drei verschiedene Verfahren angewendet:
- Laserstrahl-Brennschneiden
- Laserstrahl-Schmelzschneiden
- Laserstrahl-Sublimierschneiden
Die Art der Fertigung ist hierbei vollmechanisch oder automatisch.
Zur Fugenbildung beim Laserstrahl-Schneiden werden heute in der industriellen Fertigung fast ausschließlich Gasstrahlen verwendet. Dies können sowohl inerte oder mit dem Werkstoff chemisch reagierende sein. Sauerstoff beispielsweise reagiert mit Stoffen wie Eisen, Nickel oder Chrom stark exotherm und trägt somit neben dem Energieträger Laserstrahl als eine weitere Energiequelle zur Erwärmung bei.
Flüssigkeitsstrahlen als Schneidstrahlen weisen für einige Anwendungen erhebliche Vorteile auf und sollten daher in Betracht gezogen werden. Auch hierüber lassen sich exotherme Reaktionen mit dem Werkstück für zusätzlichen Energieeintrag nutzen. Beispielsweise kann Wasserstoff-Peroxid als Flüssigkeitsstrahl zum Austragen des Fugenstoffs eingesetzt werden und als Sauerstoffträger chemisch exotherm reagieren und somit zur Erwärmung beitragen.
Neben den Abtragverfahren, die sich in den genannten DIN-Normen auf das thermische Schneiden beziehen, wird in der Lasertechnik unter "Abtragen" auch ein eigenständiges Verfahren behandelt. [2]
Dieses Abtragen unterscheidet sich vom Schneiden dadurch, dass darüber diejenigen Bearbeitungsmethoden beschrieben werden, mit denen Bereiche von der Stoffoberfläche abgetragen werden. Der abgetragene Stoff verlässt den Grundstoff wesentlich nach oben. Im Gegensatz dazu verlässt der abgetragene Stoff beim Trennverfahren "Laserstrahlschneiden" den Grundstoff (Werkstoff) über die Schnittfuge nach unten.
Begonnen wird die Behandlung des Themas "Trennen" mit dem Kapitel Laserstrahl-Schneiden, da dieses Trennverfahren heute sehr verbreitet ist. Die physikalischen Betrachtungen sollen ein Gespür dafür entstehen lassen, welche Maßnahmen ergriffen werden können, um Verbesserungen zu erzielen oder welche neuen Wege Vorteile bringen können.
Das Laserstrahl-Schneiden
Das thermische Schneidverfahren Laserstrahlschneiden in den drei Varianten
- Laserstrahl-Brennschneiden
- Laserstrahl-Schmelzschneiden
- Laserstrahl-Sublimierschneiden
erfordert zum Schneiden der meisten Stoffe zwei Werkzeuge. Das sind erstens ein fokussierter Laserstrahl zum Fluidisieren (Schmelzen, Dampfen, Sublimieren, Zersetzen) und zweitens der Schneidstrahl zum Entfernen des Fluids. Beide wirken zusammen, um eine Schnittfuge zu erzeugen, Bild 1. Hier wird der stationäre Fall gezeigt, in dem der Laserstrahl den Stoff in der ganzen Dicke durchdringt. Dieser Fall wird erst nach einem Anlaufvorgang erreicht; denn die zu schneidenden Stoffe sind fast ausschließlich opak. Somit absorbieren sie die Laserstrahlung in der Randschicht.
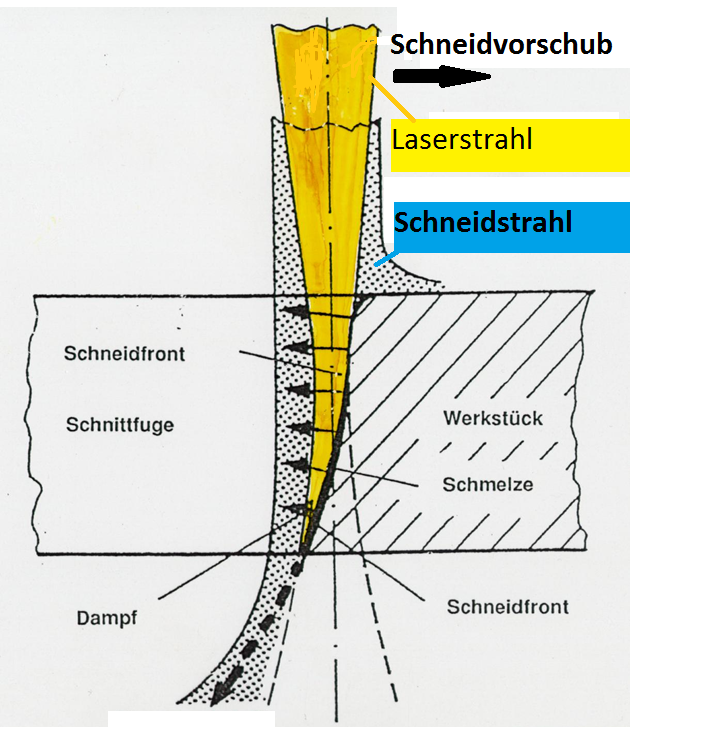
Ein fokussierter Laserstrahl erwärmt den Bereich der Schnittfuge an der Schneidfront. Der fluidisierte Stoff wird über einen Schneidstrahl aus dem Strahlbereich getrieben. Dadurch kann der fokussierte Laserstrahl auch in nicht transparenten Stoffen tief im Inneren wirken. Nach dem Durchtritt des Laserstrahls durch das zu schneidende Teil strömt der Fugenstoff nach unten aus dem Fugenbereich aus. Aufgrund des Schneidvorschubs entsteht die Schnittfuge. Der Laserstrahl erwärmt dann den Stoff nahezu ausschließlich an der Schneidfront. Als Schneidstrahl wird in der Regel ein Gasstrahl koaxial zum Laserstrahl zugeführt.
Der Anlaufvorgang kann in einem Fall so ausgeführt werden, dass der fokussierte Laserstrahl zusammen mit dem Schneidstrahl außerhalb des Stoffes startet und dann beide zusammen von der Seite her in den Stoff vorgeschoben werden. Die Schnittfuge beginnt damit am Rand. Ist dies nicht möglich, dann wird dem Schneiden ein "Lochstechen" mit oder ohne Schneidvorschub vorgeschaltet.
Zum Lochstechen erwärmt der fokussierte Laserstrahl einen eng begrenzten Bereich der Stoffoberfläche bis zum Schmelzen oder verdampft diesen. Der Schneidstrahl treibt den fluidisierten Stoff aus dem Strahlbereich überwiegend nach oben heraus. Ohne Vorschub entsteht eine Bohrung, über welche der fokussierte Laserstrahl tief in den Stoff bis zu seinem vollständigen Durchdringen eintreten kann, auch wenn dieser opak ist. Üblicherweise wird der Laserstrahl dabei über einen gewissen Zeitraum gepulst, so dass die Rate des Fluid-Transports in Richtung Schneidoptik verringert wird. Damit ist für die Optik die Gefahr eines Verschmutzens und Beschädigens niedriger. Mit eingeschaltetem Vorschub entsteht auf die gleiche Weise wie beim Bohren eine Rille, die an der Oberfläche beginnend tiefer wird und so erst nach einer kurzen Strecke den Stoff durchdringt.
Nach dem Durchtritt des Laserstrahls durch das zu schneidende Teil strömt der Fugenstoff nach unten aus dem Fugenbereich aus. Aufgrund des Schneidvorschubs entsteht die Schnittfuge. Der Laserstrahl erwärmt dann den Stoff nahezu ausschließlich an der Schneidfront. Der Schneidvorgang verläuft dann stationär, wenn die Fokussierung des Laserstrahls, die eingebrachte Laserstrahl-Leistung, die Schneidstrahl-Parameter und die Vorschubgeschwindigkeit auf die Stoffeigenschaften und die Stoffdicke abgestimmt sind.
Als Schneidstrahl wird in der Regel ein Gasstrahl koaxial zum Laserstrahl zugeführt. Ohne einen Schneidstrahl würde der aus dem erwärmten Bereich nach hinten strömende fluidisierte Stoff nach hinten (entgegengesetzt dem Schneidvorschub) strömen und die zunächst geöffnete Zone durch Kondensation und Erstarrung wieder schließen oder zumindest mit einem unerwünschten Belag die Schnittflanken verunreinigen. Das wird besonders deutlich beim Laserstrahl-Dampfschweißen (Tiefschweißen, Schlüsselloch-Schweißen, keyhole welding) von Metallen, Bild 2.
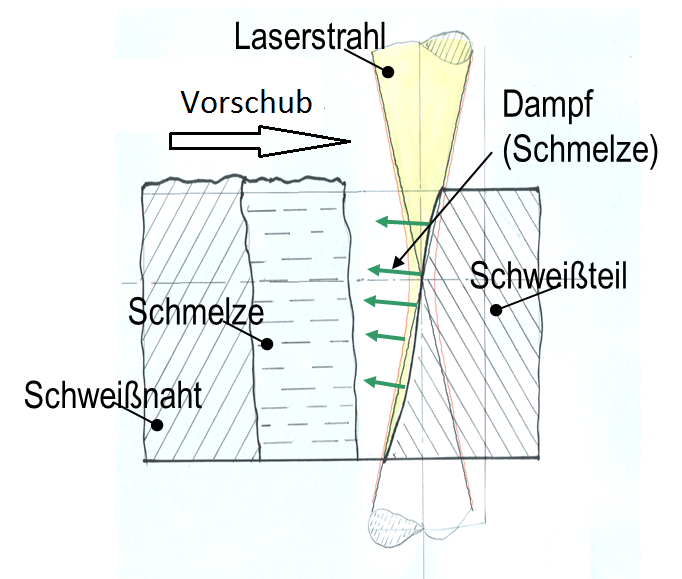
In Metallen ensteht eine Schweißnaht; denn der fluidisierte Stoff strömt von der Wechselwirkungszone zwischen Laserstrahl und Stoff nach hinten. Dort wird er letztendlich erstarren.
In diesem Fall, beim Laserstrahl-Dampfschweißen, wird gerade der Effekt genutzt, den fluidisierten Stoff wieder im festen Ausgangskörper erstarren zu lassen, so dass eine Schweißnaht entsteht und kein Schnitt. Für das Ausbilden einer Schnittfuge dagegen ist ein zweiter "Antrieb" erforderlich; denn die thermisch angetriebene Fluidströmung verlässt die Wechselwirkungszone überwiegend senkrecht zur Schneidfront, also entgegen der Vorschubsrichtung. Für das Laserstrahl-Schneiden ist also ein Ablenken der Strömung parallel zu dieser Front erforderlich damit der Fugenstoff aus dem Ausgangskörper entfernt wird. Diese Aufgabe kommt dem Schneidstrahl zu.
In Überlegungen zum Optimieren des Laserstrahlschneidens für die unterschiedlichen Anwendungen wird selten auf die Bedeutung des Schneidstrahls eingegangen. Die Hauptaufgabe des Schneidstrahls, den Fugenstoff auszutragen, ist zudem unabhängig von der Art des Laserstrahl-Schneidens. Aus diesem Grund wird hier mit den physikalischen Grundlagen des Schneidstrahls und seiner Bedeutung für die Fugenbildung nach folgender Gliederung begonnen:
↑ 1 Fugenbildung
1.1 Einfluss des Schneidstrahls auf die Fugenbildung 1.1.1 Fugenbildung mit inkompressiblen Schneidstrahlen 1.1.1.1 Angepasste Durchmesser inkompressibler Schneidstrahlen 1.1.1.1.1 Analyse der Fugenbildung im rein elastischen Stoß 1.1.1.1.2 Analyse der Fugenbildung im rein plastischen Stoß 1.1.1.1.3 Ergebnisse zur Fugenbildung mit angepassten Durchmessern inkompressibler Schneidstrahlen 1.1.1.2 Große Durchmesser inkompressibler Schneidstrahlen 1.1.1.3 Zusammenfassung der Ergebnisse zur Fugenbildung mit inkompressiblen Schneidstrahlen 1.1.2 Fugenbildung mit kompressiblen Schneidstrahlen 1.1.2.1 Angepasste Durchmesser kompressibler Schneidstrahlen 1.1.2.2 Große Durchmesser kompressibler Schneidstrahlen 1.1.2.3 Zusammenfassung der Ergebnisse zur Fugenbildung mit kompressiblen Schneidstrahlen 1.1.3 Vergleich des Einflusses inkompressibler mit kompressiblen Schneidstrahlen auf die Fugenbildung 1.2 Einbringen des Schneidstrahls in die Schnittfuge
Die verschiedenen Betrachtungen werden dahingehend ausgewertet, um Obergrenzen für die Vorschubgeschwindigkeit beim Laserstrahl-Schneiden mit unterschiedlichen Schneidstrahlen explicit anzugeben. Diese Obergrenzen lassen sich auch nicht bei beliebig hoher Leistung im Laserstrahl überwinden. Im Anschluss an die rein physikalisch begründeten Aussagen wird diskutiert, durch welche Maßnahmen diese Obergrenzen annähernd erreichen lassen.
↑ 1.1 Einfluss des Schneidstrahls auf die Fugenbildung
Der Schneidstrahl besteht grundsätzlich aus einem strömemden Fluid. Er wirkt auf den geschmolzenen oder verdampften Fugenstoff ein. Dieses Einwirken wird beschrieben, um aus seinen physikalischen Eigenschaften seinen Beitrag auf die Fugenbildung abzuleiten. Das geschieht mit Hilfe von strömungsmechanischen Gesetzen. Diese bieten sich an, da beim Schneiden auch der Fugenstoff als Fluid vorliegt. Die einfachsten fundamentalen Gesetze reichen aus, um die Grenzparameter zu finden, welche beim Schneiden eines Stoffes nicht überschritten werden können.
Von besonderem Interesse ist die höchste Schneidgeschwindigkeit, die abhängt von Kombinationen zwischen
- Stoffart,
- Schnittdicke,
- Schnittfugenbreite,
- Schneidstrahldichte,
- Vordruck in der Schneiddüse oder Schneidstrahl-Strömungsgeschwindigkeit
Diese Abhängigkeit wird in den folgenden Betrachtungen mit Hilfe physikalischer Gesetze abgeleitet.
Ziel der Betrachtungen ist, eine physikalisch gegebene Obergrenze für die Vorschubgeschwindigkeit beim Laserstrahlschneiden zu ermitteln, die sich aus den mechanischen Randbedingungen für die Ausbildung der Schnittfuge ergibt. Dabei helfen die Erhaltungssätze der klassischen Physik für Masse, Impuls und Energie. Über diese wird gezeigt, wie sich die Parameter des Schneidstrahls auf die Vorschubgeschwindigkeit beim Laserstrahlschneiden auswirken.
Der Erhaltungssatz für Masse führt zur Massenbilanz. Diese
beschreibt den Austausch der Massen eines Systems mit dessen
Umgebung. Sie besagt, dass in stationären Vorgängen (diese
werden hier für das Laserstrahlschneiden mit
kontinuierlichen Strahlen behandelt) die Stoffströme
konstant sind: 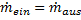
Die Impulsbilanz geht von der Impulserhaltung aus: "Der
Impuls 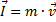 [3]
eines mechanisch abgeschlossenen Systems ist konstant". Im
Falle des Laserstrahlschneidens ist das System Schneidstrahl
– Fugenstoff nahezu abgeschlossen. Die Neigung der
Schneidfront ist dort gering, Bild 1, so dass Kräfte außer
denen zwischen Fugenstoff und Schneidstrahl vernachlässigbar
sind. Der Fugenstoff verlässt die Schnittfuge etwa parallel
zum eintretenden Schneidstrahl. Dieses geschieht unabhängig
davon, ob der fluidisierte Fugenstoff als Schmelze oder als
Dampf vorliegt. Die Volumenströme unterscheiden sich zwar,
nicht aber die Massenströme. Daher wird im weiteren Vorgehen
der Ansatz betrachtet, dass die thermische Übertragung der
Leistung aus dem Laserstrahl in das Schneidteil den gesamten
Fugenbereich vorab fluidisiert hat. Zum Ableiten einer
Obergrenze für das konventionelle Laserstrahlschneiden kann
diese Näherung gewählt werden.
[3]
eines mechanisch abgeschlossenen Systems ist konstant". Im
Falle des Laserstrahlschneidens ist das System Schneidstrahl
– Fugenstoff nahezu abgeschlossen. Die Neigung der
Schneidfront ist dort gering, Bild 1, so dass Kräfte außer
denen zwischen Fugenstoff und Schneidstrahl vernachlässigbar
sind. Der Fugenstoff verlässt die Schnittfuge etwa parallel
zum eintretenden Schneidstrahl. Dieses geschieht unabhängig
davon, ob der fluidisierte Fugenstoff als Schmelze oder als
Dampf vorliegt. Die Volumenströme unterscheiden sich zwar,
nicht aber die Massenströme. Daher wird im weiteren Vorgehen
der Ansatz betrachtet, dass die thermische Übertragung der
Leistung aus dem Laserstrahl in das Schneidteil den gesamten
Fugenbereich vorab fluidisiert hat. Zum Ableiten einer
Obergrenze für das konventionelle Laserstrahlschneiden kann
diese Näherung gewählt werden.
Unter der Voraussetzung des mechanisch abgeschlossenen
Systems heißt dies für die Fugenbildung beim
Laserstrahlschneiden: Der aus der Schneiddüse über den
Schneidstrahl in den fluiden Fugenstoff eingebrachte Impuls
ist gleich dem aus der Fuge austretenden; denn das System
ist abgeschlossen. Zusätzliche mechanische Kräfte wie
Reibungskräfte wirken auf das idealisierte System nicht ein.
Die Aussage gilt dann auch für die Impulsströme 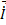 .
.
Die Energiebilanz geht von der Energieerhaltung aus: "Die Energie E eines abgeschlossenen Systems ist konstant". Unterschieden wird dabei auch zwischen Kinetischer Energie Ekin und Innerer Energie U.
In stationären Vorgängen gilt damit auch die Leistungsbilanz, da der Energiestrom als Leistung L [4] bezeichnet wird.
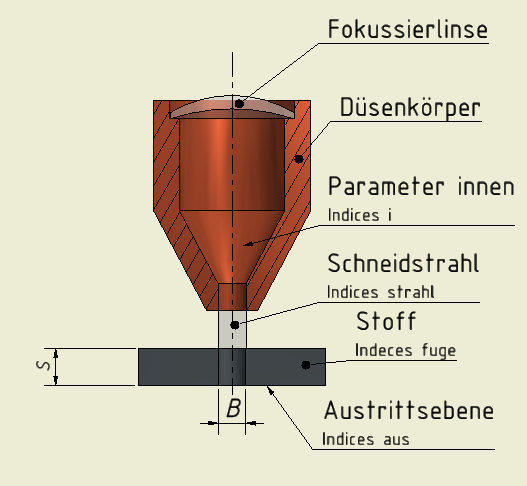
Einige Größen In den Betrachtungen haben Vektor-Charakter. Vektoren sind durch einen Pfeil über dem Grundsymbol gekennzeichnet. Zum Ermitteln von Grenzparametern reicht die Diskussion der Vektor-Komponenten in Richtung des aus der Düse austretenden Schneidstrahls aus. Daher werden hier, auch um die Schreibweise zu vereinfachen, nur die Beträge dieser Vektorkomponenten betrachtet.
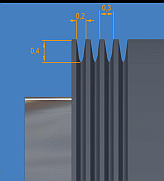
Der Schneidstrahl als Fluid wird in der Schneiddüse aufgebaut, Bild 3. Das Fluid wird in den Innenraum eingeführt und befindet sich dort in Ruhe. Der Vordruck Pi treibt es aus der Düsenmündung aus, so dass ein Schneidstrahl geformt wird.
Geometrie und Strömungsverhalten des Schneidstrahls hängen von der Kompressibilität des Schneidstrahl-Stoffs ab. Falls die Auswirkungen der Kompressibilität vernachlässigbar bleiben, wird von inkompressiblen Stoffen gesprochen. Dies trifft auf Bedingungen zu, die zu Strömungsgeschwindigkeiten führen, die klein gegenüber der Schallgeschwindigkeit des Fluids sind. So verhält sich Wasser bis zu Drücken von einigen tausend bar nahezu inkompressibel.
Gase dagegen erfordern zur Beschreibung ihres Verhaltens schon bei relativ geringfügig gegenüber der Umgebung erhöhtem Vordruck das Berücksichtigen der Kompressibilität. Der Übersichtlichkeit wegen werden inkompressibler und kompressibler Schneidstrahl getrennt behandelt.
Die Fuge entsteht dadurch, dass ein Schneidstrahl den fluidisierten Fugenstoff in Strömungsrichtung aus dem Schneidteil austrägt. Der Schneidstrahl wird in der Schneiddüse erzeugt, das Fluid im Fugenbereich durch Erwärmung mit dem Laserstrahl gebildet. Die Erzeugungsrate des Fluids ergibt sich (bei ausreichend hoher Laserleistung) wesentlich aus dem Fugenquerschnitt und der Vorschubgeschwindigkeit. Der Fugenquerschnitt ist vorgegeben, so dass die Vorschubgeschwindigkeit (Schneidgeschwindigkeit) als Variable in die Erzeugungsrate eingeht. Zum Erstellen eines Schnittes kann diese Erzeugungsrate nicht größer sein als die Austragsrate. Somit bestimmt die Austragsrate eine Grenz-Erzeugungsrate und somit die höchstmögliche Vorschubgeschwindigkeit (Schneidgeschwindigkeit). Gesucht wird die Vorschubgeschwindigkeit für die Erzeugungsrate, die noch ausgetragen werden kann.
↑ 1.1.1 Fugenbildung mit inkompressiblen Schneidstrahlen
In dem gewählten Ansatz für inkompressible Stoffe
verändert sich die Geometrie des Schneidstrahls nach dem
Austritt aus der Düse nicht, wenn Durchmischungen oder
Energieverluste durch Reibung mit dem Umgebungsstoff
vernachlässigbar sind. In dem Ansatz wird ein
rotationssymmetrischer Strahlquerschnitt betrachtet. Damit
sind Kurvenschnitte ohne weitere Maßnahmen möglich. Sein
Durchmesser d kann der Schnittfugenbreite B
angepasst werden, Bild 3. Zum besseren Verständnis der
folgenden Ableitungen werden die dort verwendeten Symbole
aufgelistet und erklärt, Tabelle 1. Der Buchstabe P,
der üblicherweise sowohl für den Druck, den Impuls und auch
für die Leistung verwendet wird, ist hier für den Druck
gewählt. Zum Vermeiden von Verwechslungen wird die Leistung
mit L gekennzeichnet, der Impuls mit I. Ein
Punkt über den Symbolen einiger physikalischer Größen zeigt
deren Ableitung nach der Zeit an. Damit werden die
Gleichungen übersichtlicher im Vergleich zu 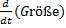 , der
ausführlichen Schreibweise.
, der
ausführlichen Schreibweise.
Tabelle 1: Verwendete Symbole
Die aufgelisteten Grundsymbole, beispielsweise v
werden durch entsprechende Indices wie "strahl"
oder "fuge" weiter spezifiziert
| Durchmesser des Schneidstrahls | d |
| Fugenbreite | B |
| Querschnittsfläche des Schneidstrahls | Astrahl |
| Querschnittsfläche des fluidisierten Fugenstoffs | Afuge |
| Dichte des Schneidstrahl-Stoffs | ρstrahl |
| Dichte des Fugenstoffs | ρfuge |
| Vordruck in der Düse | Pi |
| Strömungsgeschwindigkeit des aus der Düse austretenden Schneidstrahls | ustrahl |
| Schneidgeschwindigkeit | v |
| Masse seines Körpers | m |
| Massenstrom des Schneidstrahls | 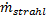 |
| Massenstrom des Fugenstoffs | 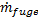 |
| Impulsstrom des erzeugten Schneidstrahls, dieser setzt sich bis zur Fuge fort | 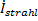 |
| Impulsstrom der austretenden Stoffe | 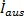 |
| Kinetische Energie eines Körpers | E |
Begonnen werden die Betrachtungen mit der Beschreibung der
mechanischen Eigenschaften der Stoffströme des
Schneidstrahls und des fluidisierten Fugenbereichs für den
Fall, dass die Durchmesser der Schneidstrahlen der
Schnittfugenbreiten angepasst sind.
1.1.1.1 Angepasste Strahldurchmesser
Stoffstrom im Schneidstrahl
Der Stoffstrom (Massestrom) des Schneidstrahls d/dt(mstrahl),
in der einfachen Schreibweise 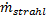 , wird in
einer Schneiddüse ausgebildet, siehe Bild 3. Sein
Querschnitt ist rund mit dem Durchmesser d. Dieser
ist angepasst an den Schneidspalt mit der Breite B.
Er ist auch etwa gleich dem Laserstrahldurchmesser. Die
Austrittsgeschwindigkeit
, wird in
einer Schneiddüse ausgebildet, siehe Bild 3. Sein
Querschnitt ist rund mit dem Durchmesser d. Dieser
ist angepasst an den Schneidspalt mit der Breite B.
Er ist auch etwa gleich dem Laserstrahldurchmesser. Die
Austrittsgeschwindigkeit 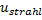 des
Schneidstrahls aus der Düse ist gleich seiner
Eintrittsgeschwindigkeit in den Schneidspalt; seine Dichte
ist
des
Schneidstrahls aus der Düse ist gleich seiner
Eintrittsgeschwindigkeit in den Schneidspalt; seine Dichte
ist 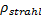 . Damit
gilt für den Massestrom des Schneidstrahls:
. Damit
gilt für den Massestrom des Schneidstrahls:
![]() (1)
(1)
![]() (2)
(2)
Der Stoff des Schneidstahls ist inkompressibel wie näherungsweise Wasser. Er befindet sich unter dem Vordruck Pi in einem Raum vor der Düse (im Kessel) und ist in Ruhe, Bild 3. Durch den Vordruck wird er aus einer Mündung ausgetrieben und formt den Schneidstrahl. Unter dieser Voraussetzung lässt sich dessen Strömungsgeschwindigkeit ermitteln zu
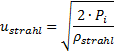 (3)
(3)
Diese Gleichung (3) ist aus der Bedingung
„Energieerhaltung“ abgeleitet worden und als
„Bernoulli-Gleichung“ bekannt. Sie gilt für anfangs ruhende
Fluide in einem Behälter unter Druck.
Stoffstrom im Fugenbereich
Der Massestrom des fluidisierten Fugenbereichs d/dt(mfuge)
– in der einfachen Schreibweise 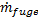 – hat
seinen Ursprung im Schneidteil. Er wird bestimmt durch den
Schneidvorschub v mit dem sich der Schneidstrahl
durch das Schneidteil der Dichte
– hat
seinen Ursprung im Schneidteil. Er wird bestimmt durch den
Schneidvorschub v mit dem sich der Schneidstrahl
durch das Schneidteil der Dichte 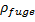 bewegt,
sowie über die Abmessungen des Spaltes der Breite B
und der Dicke S, Bild 4, zu:
bewegt,
sowie über die Abmessungen des Spaltes der Breite B
und der Dicke S, Bild 4, zu:
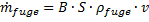 (4)
(4)
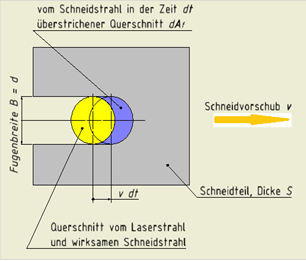
Fluidisieren des Fugenstoffs
Fluidisiert wird der Fugenbereich durch den Laserstrahl, der sich mit der konstanten Geschwindigkeit v linear über das Schneidteil der Dicke S bewegt. In der Zeit dt wird dabei ein Volumen unter dem Querschnitt dAf (blau hinterlegt) fluidisiert. Dieser fluidisierte Bereich wird von dem Schneidstrahl mit rundem Querschnitt aus der Fuge ausgetrieben. Ein runder Querschnitt wird gewählt, da Kurvenschnitte ohne Zusatzachse (Drehachse δ in der Schneidanlage) zum Stand der Technik gehören. Als Modell für die Berechnungen ist hier der Ansatz gewählt, dass der Fugenbereich auch ohne Laserstrahl schon vor dem Austragen als Fluid vorliegt.
Der Vorgang "Fugenbildung" lässt sich in zwei Grenzfällen betrachten. Im ersten Grenzfall ist der Schneidstrahldurchmesser Am Ort des Schneidteils der Fugenbreite angepasst. Hier helfen neben den Gesetzen zur Massenerhaltung die Betrachtung der Stoßgesetze für den rein elastischen und für den rein plastischen Stoß weiter.
Der zweite hier behandelte Grenzfall bezieht sich auf die Auswirkung von Schneidstrahlen, deren Durchmesser sehr viel größer als die Schnittfugenbreiten sind. Hier erleichtern neben der Betrachtung der Stoffströme, die Bernoulli-Gleichungen (Umwandlung von Druck in Geschwindigkeit von Fluiden – und umgekehrt) das Finden von Aussagen zur Begrenzung der Schneidgeschwindigkeit aufgrund der Schneidstrahl-Eigenschaften.
Wirken des Schneidstrahls auf den Fugenstoff
Der Schneidstrahl wirkt auf den fluidisierten Fugenstoff ein, Bild 3, beschleunigt ihn auf die Austrittsgeschwindigkeit uaus und treibt ihn so aus. Der Vorgang lässt sich in zwei Grenzfällen über Stoßgesetze berechnen. Der eine Grenzfall behandelt den rein elastischen Stoß. Dabei wird der Schneidstrahlimpuls vollständig – ohne Umwandlung von kinetischer Energie in innere Energie – auf den Fugenstoff übertragen. Das ist ein absoluter Grenzfall, der beim Laserstrahl-Schneiden nicht erreicht wird. Damit aber wird eine Grenze aufgezeigt, die nicht überschritten werden kann.
Der zweite Grenzfall ist der rein inelastische Stoß mit Impuls- und Energieübertragung zwischen Schneidstrahl und Fugenstoff. In diesem Fall verlassen Schneidstrahl und Fugenstoff die Fuge gemeinsam mit gleicher Strömungsgeschwindigkeit. Dies ist beispielsweise der Fall beim autogenen Brennschneiden wenn der Schneidstrahl mit dem Fugenstoff vollständig chemisch reagiert. In diesem zweiten Fall wird ein Teil der aus dem Schneidstrahl in die Fuge eingebrachten kinetischen Energie in innere Energie der austretenden Stoffe transformiert.
Allgemein wird das Laserstrahlschneiden zwischen den beiden Grenzfällen ablaufen, wobei eine Vielzahl weiterer Parameter die Fugenbildung beeinflusst.
Der Schneidstrahlquerschnitt ist in dem hier gewählten Ansatz der Fugenbreite angepasst. Voraussetzung in dieser Betrachtung ist, dass die Laserleistung zur Fluidisierung ausreicht.
1.1.1.1.1 Analyse der Fugenbildung im rein elastischen Stoß
Die Schnittfuge entsteht durch strömende Fluide, die aufeinander einwirken und zusätzlich noch an Fugenwänden und an der umgebenden Atmosphäre reiben. Diese Reibungseffekte behindern den Austrag des Fugenstoffs aus dem Schnittbereich. Eine Obergrenze wird gesucht, daher werden Reibung und auch andere Effekte, welche die Strömung der Stoffe behindern, nicht berücksichtigt.
Die Analyse der Übertragung von Impuls und kinetischer Energie des Schneidstrahls auf den Fugenstoff lässt sich auf die Bewegung zweier sich stoßender Massen vereinfachen. Hierzu werden die Stoßgesetze für zwei Massen m1 und m2 mit deren Geschwindigkeiten vor dem Stoß u1,vor und u2,vor im rein elastischen linearen Stoß hinzugezogen. Beim Laserstrahlschneiden entspricht die stoßende Masse m1 der des Schneidstrahls, die Masse m2 der des Fugenstoffs. Die Stoßgleichungen vereinfachen sich für den Fall, dass die Geschwindigkeitskomponente in Strahlrichtung der Masse m2 vor dem Stoß null ist.
Begonnen wird mit den Erhaltungssätzen für Impuls und
Energie. Der Stoß ist dann rein elastisch, wenn während des
Stoßes ausschließlich Anteile von kinetischer Energie
übertragen werden. Eine Transformation in Wärme- oder andere
Energien findet nicht statt, weder in die stoßenden Massen
noch in die Umgebung. Zunächst die Definitionen für Impuls
und kinetischer Energie von Massen der Geschwindigkeit 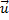 .
.
Definition Impuls einer Masse
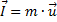 (5)
(5)
Definition Kinetische Energie einer Masse
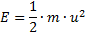 (6)
(6)
Die Gesetze Impulserhaltung und Energieerhaltung bedeuten „Gesamtimpuls vor dem Stoß ist gleich Gesamtimpuls nach dem Stoß“ und im gewählten Fall einer verlustlosen Energieübertragung auch „kinetische Gesamt-Energie vor dem Stoß ist gleich kinetischer Gesamt-Energie nach dem Stoß“. Die Gesetze sind über die Definitionen Gleichung (6) und Gleichung (7) formuliert und ergeben für eine anfangs ruhende Masse m2:
Impulserhaltung beim Stoß von m1 auf anfangs ruhende Masse m2
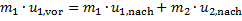 (7)
(7)
Energieerhaltung beim Stoß von m1 auf anfangs ruhende Masse m2
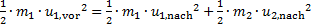 (8)
(8)
Diese Gleichungen (7) und (8) werden für weitere Auswertungen umformuliert: Aus (7) folgt
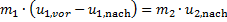 (9)
(9)
Aus (8) folgt
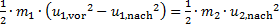 (10)
(10)
Aus diesen Gleichungen (9) und (10) für die Impuls- und Energiebilanzen ergeben sich die Zusammenhänge der Geschwindigkeiten beider Massen vor und nach dem Stoß durch Teilen von Gleichung (10) durch Gleichung (9). Die Geschwindigkeiten beider Massen nach dem Stoß sind
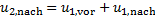 (11)
(11)
oder
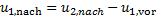 (12)
(12)
Mit Hilfe dieser Geschwindigkeitsbeziehungen liefert der Impulserhaltungssatz Gleichung (10) die Geschwindigkeiten der beiden Massen nach dem Stoß wie folgt:
Aus (11) in (7) wird
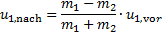 (13)
(13)
Aus (12) in (7) wird
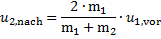 (14)
(14)
Damit sind die kinetischen Größen explicit bekannt und eine Bilanz der Energie vor dem Stoß im Vergleich zur Energie nach dem Stoß kann für beide Massen ausgeführt werden. Für die Masse m1 folgt über die Definitionsgleichung (6): Abgabe der kinetischer Energie von m1 über den Stoß
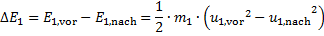 (15)
(15)
Mit (13) wird aus (15) die Abgabe von kinetischer Energie von m1 über den Stoß:
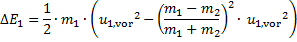 (16)
(16)
Gleichung (16) vereinfacht
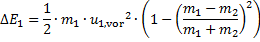 (17)
(17)
Gleichung (17) beschreibt die absoluter Änderung der
kinetischen Energie der Masse m1 durch
den Stoß mit Masse m2. Diese absolute
Änderung wird im nächsten Schritt auf die Eingangsenergie
bezogen und damit relativiert. Diese relative Änderung  ergibt aus
Gleichung (17) mit der Definition (6) die Gleichung (18)
ergibt aus
Gleichung (17) mit der Definition (6) die Gleichung (18)
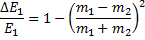 (18)
(18)
Der Höchstwert einer Übertragung von relativer kinetischer Energie aus einer Masse m1 ist 1, da Energiegewinn nicht möglich ist.
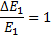 (19)
(19)
Dieser ist nach Gleichung (18)
mit m1 = m2 erreicht. Die Bedingung für die höchstmögliche Energieübertragung im elastischen Stoß zweier Massen ist somit
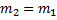 (20)
(20)
Das Ergebnis aus der vereinfachten Betrachtung über den rein elastischen Stoß zweier Massen wird auf die Bedingungen beim Vorgang „Laserstrahlschneiden“ übertragen, indem die Massen durch Stoffströme ersetz werden. Das ist möglich, da das stationäre Laserstrahlschneiden untersucht wird. Hier wirkt der Laserstrahl im kontinuierlichen Modus mit konstanter Leistung auf das Schneidteil ein, und der Schneidstrahl strömt kontinuierlich mit unveränderten Parametern. Die weitere Bedingung, lineare Zusammenhänge in den Gleichungen, ist ebenfalls erfüllt.
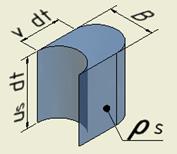
Massenstrom des Schneidstrahls
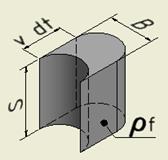
Stoffstrom im Schneidspalt
In den Stoffströmen werden hier Massenelemente betrachtet. Ein Massenelement des Schneidstrahlstroms, der mit v über das Werkstück bewegt wird, ist nach Bild (5) und Bild (6) beschrieben zu
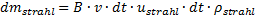 (21)
(21)
Ein Massenelement des Strom des Fugenstoffs nach Bild (3) und Bild (5)
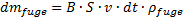 (22)
(22)
Die Stoßgesetze gelten für jede Massen und somit auch für die Massenelemente. Daher folgt der Maximalwert für eine Übertragung der kinetischen Energie aus dem Schneidstahl auch der Gleichung (20) und ergibt
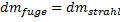 (23)
(23)
Das Maximum des eintretenden Stoffstrahls wird durch die
Abmessung des Schneidstrahls in Vorschubrichtung bestimmt.
Dieser ist rund. Das führt dann zu 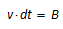 und damit
zu
und damit
zu
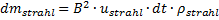 (24)
(24)
Die Bedingung für eine maximale Übertragung von kinetischer Energie im elastischen Stoß zwischen Schneidstahl und Fugenstoff, Gleichung (23), ergibt damit
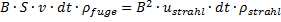 (25)
(25)
Gleichung (25) wird nach v aufgelöst
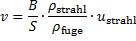 (26)
(26)
Mit Gleichung (26) ist eine Aussage für die Parameter zum Laserstrahlschneiden gefunden, welche die höchstmögliche Vorschubgeschwindigkeit ergeben, wenn mit inkompressiblen Schneidstrahlen, die der Fugenbreite angepasst sind, geschnitten wird. Die Gleichung zeigt einfache Zusammenhänge zwischen den einzelnen Parametern.
Die Austrittsgeschwindigkeit ustrahl wird üblicherweise nicht als Betriebsparameter verwendet. Betriebsparameter ist gewöhnlich der Vordruck Pi. Der Zusammenhang ist aus Gleichung (3) bekannt. Damit ist die Obergrenze der Vorschubgeschwindigkeit (die Grenzgeschwindigkeit) beim Laserstrahlschneiden formuliert als Gleichung (27) Grenzgeschwindigkeit bezogen auf den Betriebsparameter Vordruck
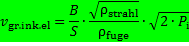 (27)
(27)
Die absolute Obergrenze für die Vorschubgeschwindigkeit beim Laserstrahlschneiden mit inkompressiblen Schneidstahlstoffen wird also direkt bestimmt über das Aspektverhältnis S/B und über die Dichte des zu schneidenden Stoffes. Sie ist umgekehrt proportional zum Aspektverhältnis und umgekehrt proportional zur Dichte des Schneidteils. Höhere Dichten des Schneidstrahls und höhere Vordrücke in der Schneiddüse erhöhen die Grenzgeschwindigkeit über den Exponenten 1/2.
Von Interesse könnte auch eine Formulierung der Obergrenze für die Wahl eines bestimmten Lasertyps sein; denn das Aspektverhältnis der Schnittfuge wird über die Kaustik des Laserstrahls bestimmt.
Das Verhältnis B/S einer Schnittfuge mit etwa parallelen Schnittflanken – und damit auch bei optimaler Nutzung der Laserstrahlleistung – wird aus der Bilanz zwischen Laserstrahlleistung und thermischer Leistung für die Fluidisierung abgeleitet. Für einen Laserstrahl mit der Strahlinvarianten Ki und der Dicke S des Stoffs, der bearbeitet wird, ist der optimale Fokusdurchmesser und damit die optimale Fugenbreite Bopt die Gleichung
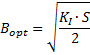 (28)
(28)
Aus (28) durch Division mit S wird das Verhältnis Bopt / S :
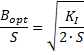 (29)
(29)
Damit ist für ein Laserstrahlschneiden mit einem Laserstrahl der Invarianten Ki die Obergrenze der Schneidgeschwindigkeit nach Gleichung (30) gegeben.
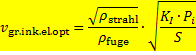 (30)
(30)
Schneller kann also aufgrund der Fugenbildung mit runden Schneidstrahlen, die der Fugenbreite angepasst sind, nicht geschnitten werden – unabhängig davon, wie hoch die Laserstrahlleistung gewählt wird. Die Strahlinvariante Ki ist proportional zur Wellenlänge des Laserstrahls und steigt mit der transversalen Modenordnung.
1.1.1.1.2 Analyse der Fugenbildung im rein plastischen Stoß
Im rein plastischen Stoß zwischen zwei inkompressiblen Medien der Massen m1 und m2 der Geschwindigkeiten vor dem Stoß u1 und u2 bewegen sich beide Medien nach dem Stoß mit gleicher Geschwindigkeit unach; sie „kleben“ praktisch aneinander. Die Gesetze Impulserhaltung und Energieerhaltung über die Definitionen (6) und (7) ergeben für den Fall der vor dem Stoß ruhenden zweiten Masse m2 Impulserhaltungssatz im Stoß mit anfangs ruhender Masse m2
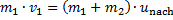 (31)
(31)
Energieerhaltungssatz im Stoß mit anfangs ruhender Masse m2
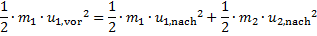 (32)
(32)
Gleichung (32) liefert für die gemeinsame Geschwindigkeit unach der beiden Massen m1 und m2 nach dem Stoß: Geschwindigkeiten beider Massen nach dem voll plastischen Stoß
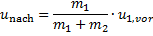 (33)
(33)
Mit Hilfe der Gleichungen zur Geschwindigkeit, Impuls und Energie wird nun eine Bedingung gesucht, die bei vorgegebener Masse und Geschwindigkeit des stoßenden Körpers zur höchsten Geschwindigkeit und Masse des gestoßenen Körpers nach dem Stoß führt. Dazu wird die Energiebilanz betrachtet und aus dieser bestimmt, wo das Maximum für eine relative Änderung der kinetischen Energie der Masse m2 liegt. Die relative Änderung der kinetischen Energie von Masse m2 ist hier, da die Masse m2 vor dem Stoß ruht
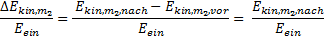 (34)
(34)
Relative Änderung der kinetischen Energie der anfangs ruhende Masse m2
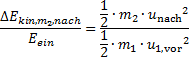 (35)
(35)
In dieser Gleichung (35) sind m1 und u1,vor vorgegeben, m2 wird gesucht und unach ist aus Gleichung (33) bekannt. Damit führt das relative Verhältnis der Energien zum einfachen Verhältnis der beiden Massen, Gleichung (36).
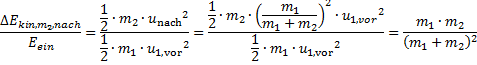 (36)
(36)
Gesucht wird die höchstmögliche relative Energieübertragung aus der Masse m1 in die Masse m2. Diese wird mit Hilfe der bekannten Methode zur Extremwertberechnung ermittelt, Gleichung (37).
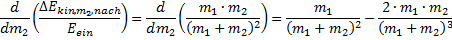 (37)
(37)
Die Nullstelle von 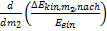 liegt bei
liegt bei
m1 = m2 (38)
Sie zeigt ein Maximum an; denn die Analyse von Gleichung
(35) zeigt für jedes 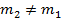 eine geringere Übertragung der relativen kinetischen
Energie. Daraus folgt, dass mit jeder Abweichung der
Bedingung m1 = m2 die
Geschwindigkeit der Masse m2 nach dem
Stoß verringert wird.
eine geringere Übertragung der relativen kinetischen
Energie. Daraus folgt, dass mit jeder Abweichung der
Bedingung m1 = m2 die
Geschwindigkeit der Masse m2 nach dem
Stoß verringert wird.
Die optimalen Massenverhältnisse zur Energieübertragung im voll plastischen Stoß, Gleichung (37), stimmen mit denen im rein elastischen Stoß, Gleichung (20), überein. Also folgen auch die Massenströme bei der Fugenbildung den gleichen Gesetzen.
Somit ist die absolute Obergrenze der Vorschubgeschwindigkeiten beim Laserstrahlschneiden mit inkompressiblen Schneidstrahlen gefunden: Die Grenzgeschwindigkeit für ein Verhältnis der Fugenbreite B zur Schnittdicke S bezogen auf den Betriebsparameter "Vordruck" ist
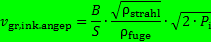 (39)
(39)
Die Grenzgeschwindigkeit bezogen auf die Invariante des Laserstrahls ist für die Schnittdicke S und den Vordruck Pi
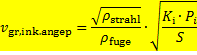 (40)
(40)
Voraussetzung in der Bestimmung dieser Grenz-Vorschubgeschwindigkeiten ist ein inkompressibler Schneidstrahl mit rundem Querschnitt, dessen Durchmesser der Schnittfugenbreite entspricht.
1.1.1.1.3 Ergebnisse zur Fugenbildung mit inkompressiblen Schneidstrahlen angepasster Durchmesser
Behandelt wurde das Laserstrahlschneiden mit inkompressiblen Schneidstrahlen, deren Durchmesser an die Schnittfugenbreite angepasst sind. Berechnungen zur Begrenzung der Schneidgeschwindigkeit aufgrund der Bedingung, dass der Fugenstoff aus dem Fugenbereich entfernt werden muss, um einen Schnitt zu erzeugen, wurden über Stoßgesetze für zwei Grenzbetrachtungen durchgeführt. Ein Grenzfall ist der voll elastische Stoß, der andere der voll plastische. In beiden Fällen wurde der Schneidstrahl mit rundem Durchmesser an die Fugenbreite angepasst. Beide Grenzfälle führen zur gleichen höchstmöglichen Vorschubgeschwindigkeit. Die Obergrenze steigt proportional zur Fugenbreite an und sinkt im gleichen Maße mit der Schnittdicke. Das Verhältnis B/S der Schnittfuge geht somit proportional auf die Obergrenze der Schneidgeschwindigkeit ein. Ebenso direkt verringert die Dichte des Fugenstoffs diese Grenze. Die Dichte des Schneidstrahls und der Vordruck in der Schneiddüse erhöhen die Grenze mit dem Exponenten 1/2.
Ein Unterschied zwischen beiden Grenzfällen sollte jedoch beachtet werden: Im rein plastischen Stoß ist die Austrittsgeschwindigkeit des Fugenstoffs nur halb so hoch wie im rein elastischen Stoß, vergleiche Gleichung (33) mit Gleichung (13). Dies bedeutet, dass beim Aufschmelzen des Fugenstoffs mit dem Laserstrahl, die Dicke δ der Schmelze im rein plastischen Fall doppelt so groß ist wie im rein elastischen Fall.
Auf den Einfluss der Schichtdicke δ auf die Erwärmung wird im entsprechenden Kapitel eingegangen. Einen Eindruck über den Einfluss der Bearbeitungsparameter auf die Obergrenze der Schneidgeschwindigkeit vermittelt die folgende Beispielsrechnung.
Beispielsrechnung für das Schneiden von Stahl mit einem Schneidstrahl aus Wasser. Die Fugenbreite ist optimiert für den Grundmode eines Nd-Laserstahls.
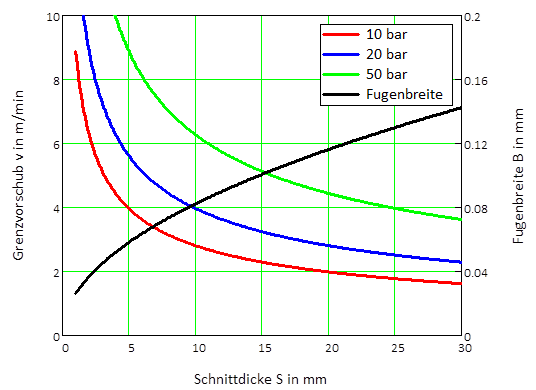
Beachtet werden sollte, dass diese berechneten Ergebnisse für angepasste Schneidstrahlen mit runden Querschnitten gelten, deren Durchmesser der Fugenbreite entsprechen. Der runde Querschnitt des Schneidstrahls wurde gewählt, damit der Schneidstrahl den fluidisierten Fugenstoff auch in Kurvenschnitten aus der Fuge entfernen kann, bevor dieser an den Schnittflanken erstarrt. Schneidstrahlen mit deutlich größeren Durchmessern werden durch die Fuge "abgeschält". Damit ist die Breite des Schneidstrahls zwar die Fugenbreite, dessen Ausdehnung in Fugenrichtung kann jedoch größer als B sein. Damit erhöht sich auch die Grenz-Vorschubgeschwindigkeit. Wo die erweiterte Grenze liegt, wird in einem weiteren Ansatz untersucht.
Für Geradschnitte, wie sie beispielsweise beim Besäumen von Bandprodukten infrage kommen, kann die Schneidstrahlabmessung in Vorschubrichtung größer sein als B, ohne dass der Schneidstrahl am Eindringen in die Fuge gehindert wird. Sie kann eine beliebige Länge L aufweisen. Damit ist v·d t = L. Wird dies beachtet, dann führen Gleichungen (21) bis (27) zu Gleichung (41). Diese beschreibt höchstmögliche Schneidgeschwindigkeit in Linearschnitten.
 (41)
(41)
Die Schneidgeschwindigkeit in Linearschnitten kann also gegenüber der in Kurvenschnitten um den Faktor L / B höher sein.
1.1.1.2 Große Strahldurchmesser
Falls der Schneidstrahl-Durchmesser groß gegen die Fugenbreite gewählt wird, wird dessen Strom beim Auftreffen auf die Oberfläche des Schneidteils im Wesentlichen parallel zu dieser abgelenkt; er breitet sich im Wesentliche seitlich aus. Die Komponente seines Impulsvektors in Schneidstrahl-Strömungsrichtung wird in einen Kraftsoß umgewandelt und geht gegen null. Aus dieser Impulsänderung baut sich ein Staudruck in Höhe des Vordrucks Pi auf.
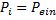 (42)
(42)
Somit kann der Raum oberhalb des Schneidteils als Raum mit dem Vordruck der Schneiddüse betrachtet werden. Dieser treibt den fluidisierten Fugenstoff aus. Mit diesem Ansatz ergibt sich für den austretenden Stoffstrom nach Bernoulli entsprechend Gleichung (3) die Austrittsgeschwindigkeit uaus
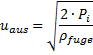 (43)
(43)
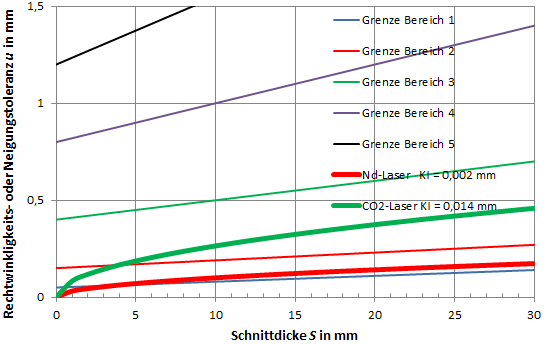
Über diese Austrittsgeschwindigkeit lässt der Stoffstrom ermitteln, wenn der Strömungsquerschnitt bekannt ist. Eine Dimension des Strömungsquerschnitts ist die Fugenbreite B. Die zweite Dimension, die Dicke des strömenden Fluids, Ist noch nicht bekannt. Sie wird hier bestimmt sich über die gewünschte Schnittqualität; denn mit größerem Querschnitt des austretenden Stoffstroms dringt dieser weiter in die schon erzeugte Schnittfuge ein. Dort kann er an den Schnittflanken kondensieren oder erstarren. Die Schnittgüte wird dadurch vermindert. Aus Forderungen, in denen eine Schnittqualität erreicht wird, die dem Stand der Technik heute entspricht, sollte die Ausdehnung δ der austretenden Stoffströme in Richtung Schneidspalt auf Abmessungen der Schnittfugenbreite beschränkt werden. Damit bleiben dann die Rechtwinkligkeits- oder Neigungstoleranzen auch in Kurvenschnitten innerhalb der Bereiche 1 bis 3 nach EN ISO 9013, Bild 7.
Das Kriterium "Schichtdicke δ des austretenden Fugenstoffs gleich Fugenbreite B" wird in die Diskussion einbezogen. Die Volumenkonstanz für den fluidisierten Fugenstoff besagt
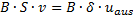 (44)
(44)
Mit B = δ folgt hieraus
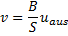 (45)
(45)
Mit der bekannten Austrittsgeschwindigkeit, Gleichung (41), wird für den Fall eines großen Schneidstrahl-Querschnitts die Grenz-Vorschubgeschwindigkeit
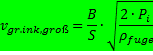 (46)
(46)
Diese für große Schneidstrahlquerschnitte ermittelte
Grenzgeschwindigkeit ist höher als diejenige, die bei gleichem Vordruck mit
angepasstem Schneidstrahldurchmesser erzielt werden kann.
Das Verhältnis zwischen beiden Fällen, Gleichung (46) zu
Gleichung (40), ergibt eine um den Faktor 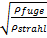 höhere
Grenzgeschwindigkeit für das Schneiden mit großen
Schneidstrahldurchmessern. Beim Schneiden von Stahl mit
einem Schneidstrahl aus Wasser kann also mit großen
Schneidstrahldurchmessern um einen Faktor 2,8 schneller
geschnitten werden als mit angepassten. Die erreichbaren
Schneidgeschwindigkeiten mit inkompressiblen Schneidstrahlen
großer Durchmesser sind als Übersicht berechnet,
Bild 9.
höhere
Grenzgeschwindigkeit für das Schneiden mit großen
Schneidstrahldurchmessern. Beim Schneiden von Stahl mit
einem Schneidstrahl aus Wasser kann also mit großen
Schneidstrahldurchmessern um einen Faktor 2,8 schneller
geschnitten werden als mit angepassten. Die erreichbaren
Schneidgeschwindigkeiten mit inkompressiblen Schneidstrahlen
großer Durchmesser sind als Übersicht berechnet,
Bild 9.
Für eine Interpretation des Berechnungsbeispiels sollte beachtet werden, dass die Schnittfugenbreiten über die Optimierung aus der thermischen Leistungsbilanz ermittelt wurden. In diese Berechnungen zum Laserstrahlschneiden mit Nd-Laserstrahlen im Grundmode ist damit das größtmögliche Aspektverhältnis (S/B) eingegangen.
1.1.1.3 Zusammenfassung der Ergebnisse zur Fugenbildung mit
inkompressiblen Schneidstrahlen
Die Grenz-Vorschubgeschwindigkeit (höchstmögliche Schneidgeschwindigkeit), die auch bei beliebig hoher Leistung im Laserstrahl nicht überschritten werden kann, wurde erechnet für inkompressible Schneidstrahlen, wie sie beispielsweise mit Wasserstrahlen verwirklicht werden können. Hierbei wurde der Fall behandelt, dass der Durchmesser des Schneidstrahls der Fugenbreite des Schnittes entspricht (ein angepasster Schneidstrahl) und der Fall, dass der Durchmesser sehr viel größer als die Schnittfugenbreite ist.
Bei angepasstem Schneidstrahl ist die Grenzgeschwindigkeit unabhängig davon, ob der Fugenstoff mit rein elastischer Wechselwirkung oder in rein plastischer Ankopplung an den Schneidstrahl ausgetrieben wird. Die Grenzgeschwindigkeit hängt direkt vom Verhältnis der Fugenbreite zur Schnittdicke ab und steigt umgekehrt proportional mit der Dichte des Fugenstoffs. Die Dichte des Schneidstrahl-Stoffs geht mit der Wurzel in die Grenzgeschwindigkeit ein, ebenso wie der Vordruck in der Schneiddüse.
Bei vorgegebener Schnittdicke steigt die Grenze proportional zur Fugenbreite. Allerdings wird die Fugenbreite vom eingesetzten Laserstrahl bestimmt. Wird dessen Fokussierung optimiert, dann bestimmt die Strahl-Invariante die Schnittfugenbreite, so dass die Grenz-Schneidgeschwindigkeit mit größerer Strahlinvariant steigt und zwar proportional zur Quadratwurzel aus der Strahlinvarianten.
Mit großen Schneidstrahldurchmessern lassen sich bei gleichem Vordruck und gleichem Verhältnis der Fugenbreite zur Schnittdicke höhere Schneidgeschwindigkeiten erzielen. Diese sind dann unabhängig von der Dichte des Schneidstrahl-Stoffs. Die Dichte des Fugenstoffs allerdings geht unter der Wurzel ein. Eine höhere Dichte erniedrigt die Grenzgeschwindigkeit nicht in dem Maße, wie bei angepasstem Sschneidstrahl-Durchmesser.
↑ 1.1.2 Fugenbildung mit kompressiblen Schneidstrahlen
Das Laserstrahl-Schneiden ist heute als Standardverfahren eingeführt. Industrielle Anwendungen verwenden CO2-Laserstrahlen. In der Regel werden Schneidstrahlen aus den Gasen Stickstoff oder Sauerstoff verwendet. Gase sind leicht komprimierbar. Sie ändern bei Druckänderungen sowohl das Volumen als auch ihre Temperatur. Damit hängt deren Dichte von den anderen Zustandsgrößen ab. Zudem ist die Schallgeschwindigkeit ein Kriterium, welches das Erzeugen und den Verlauf von Gasstrahlen wesentlich bestimmt.
Die leichte Komprimierbarkeit von Gasen führt dazu, dass Die Schallgeschwindigkeit in diesen Stoffen vergleichsweise niedrig liegt. Die Schallgeschwindigkeit begrenzt den Stofftransport in Mündungen oder Düsen; denn die Strömungsgeschwindigkeit eines Gases kann im engsten Querschnitt am Ausgang eines Raumes, höchstens Schallgeschwindigkeit annehmen. Höhere Strömungsgeschwindigkeiten erfordern eine Expansion des Gases nach dem engsten Querschnitt. Diese kann gezielt in der Düse erfolgen oder auch durch Nachexpansion im Freistrahl. Eine sich erweiternde Düse wird Lavaldüse genannt.
Zum Abschätzen der Grenzbedingungen für das Schneiden mit kompressiblen Schneidstrahlen wird eine angepasste Lavaldüse zugrunde gelegt, Bild 10 und Bild 11; denn in dieser lassen sich Schneidstrahlen verlustfrei formen. Ein derart geformter Schneidstrahl wirkt daher mit dem höchsten Impulsstrom und dem höchsten Strom kinetischer Energie auf den Fugenstoff ein.
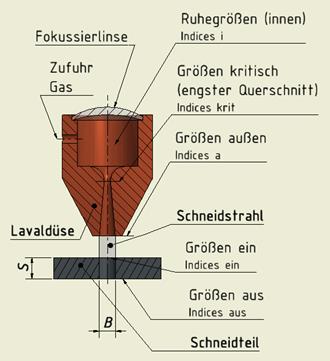
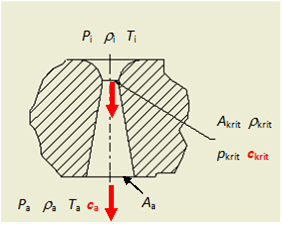
Bild 11: Bezeichnungen von Größen in der Lavaldüse
für die Berechnungen
A: Querschnittsfläche;
κ: Isentropenexponent;
P: Druck;
Ma: Machzahl;
Indices:
krit: im engsten Querschnitt;
a: außerhalb der Düse;
i: innerhalb ruhend
Das Verhalten von kompressiblen Schneidstrahlen wird über gasdynamische Gesetze beschrieben. Diese werden Zu Beginn aufgelistet, Tabelle 2.
Tabelle 2: Auflistung gasdynamischer Gesetze zur Lavaldüse
| Formelzeichen in der Tabelle | ρ: Dichte des Gases P: statischer Druck des Gases T: Temperatur des Gases Rs: spezielle Gaskonstante c: Schallgeschwindigkeit κ: Isentropenexponent Ma: Machzahl A: Querschnittsfläche |
|
|
| Indices | i: innen a: außen krit: im kritischen (engsten) Querschnitt |
|
|
| Dichte eines Gases | 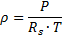 |
Aus der Zustands-gleichung für ideale Gase |
(47) |
| Schallgeschwindigkeit im Druckraum |
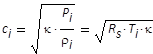 |
Hütte E 154 (8) |
(48) |
| Kritische Schallgeschwindigkeit | 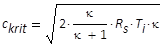 |
aus (48) mit (51) |
(49) |
| Machzahl (Verhältnis der Strömungs-geschwindigkeit zur Schallgeschwindigkeit, hier Ma in der Umgebung) | 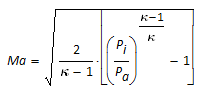 |
Dubbel 1961, Seite 319 |
(50) | Kritisches Temperaturverhältnis | 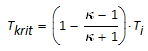 |
Nach Hütte E 160 (31) |
(51) |
| Kritisches Druckverhältnis | 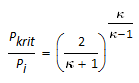 |
Nach Hütte E 160 (31) und (32) |
(52) |
| Kritisches Dichteverhältis | 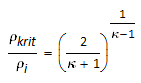 |
Hütte E 160 (31) und (32) | (53) |
| Kritisches Querschnittsverhältnis | 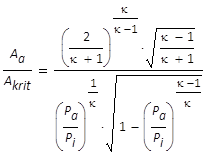 |
Hütte E 161 (33) |
(54) |
| Näherung für den Staudruck mit Verlusten | 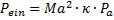 |
Dubbel 1961, Seite 321 |
(55) |
1.1.2.1 Angepasste Durchmesser kompressibler Schneidstrahlen
Die Erhaltungssätze für Impuls und Energie führten zu der Aussage, dass die Massenströme des Schneidstrahls und des Fugenstoffs gleich sind, wenn die Schneidstrahldurchmesser an die Fugenbreite angepasst sind, Gleichung (23). Diese Aussage ist unabhängig von weitern Bedingungen. Daher gilt sie auch für kompressible Schneidstrahlen. Für die angepassten Durchmesser wird im ersten Schritt die Grenzgeschwindigkeit für das Schneiden ermittelt.
Aus Gleichung (54) ergibt sich der kritische Querschnitt der Lavaldüse, dessen Durchmesser sich nach Expansion des Strahls zur Fugenbreite B aufweitet, Gleichung Gleichung (56)
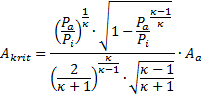 (56)
(56)
Hierin ist der Strahlquerschnitt am Düsenausgang Aa = B·v·dt, Bild 3. Seine größtmögliche Abmessung v·dt kann höchstens den Durchmesser des Austretenden Strahls d = B annehmen, so dass Aa = B2 die größte Querschnittsfläche des austretenden Schneidstrahls darstellt.
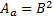 (57)
(57)
In der kritischen Querschnittsebene, Bild 11 herrscht der Druck Pkrit. Dieser ergibt sich nach Gleichung (53) aus der Dichte im Inneren ρi zu
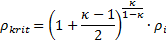 (58)
(58)
Die Dichte des Gases im Inneren wird nach Gleichung (47) bestimmt zu
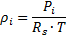 (59)
(59)
Mit der Schallgeschwindigkeit im kritischen Querschnitt ckrit , Gleichung (49), sind dann alle Größen bekannt, die den Stoffstromaus der Lavaldüse bestimmen. Dieser ist entsprechend Gleichung (22)
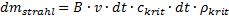 (60)
(60)
Der Massenstrom des Fugenstoffs ist aus Gleichung (23) bekannt, so dass die Gleichheit der Ströme Fugenstoff – Schneidstrahl analog zu Gleichung (26) die die Bilanzgleichung (60) ergibt.
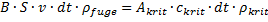 (61)
(61)
Gleichung (61) aufgelöst nach v unter Verwendung der Gleichungen (54) bis (59) ergibt die gesuchte Lösung für den behandelten Fall, dass der Schneidstrahldurchmesser eines kompressiblen Stoffs an die Schnittfugenbreite angepasst ist, Gleichung (62).
 (62)
(62)
Der Einfluss der Betriebsparameter auf die Grenzgeschwindigkeit ist bei kompressiblen Schneidstrahlen mit angepassten Durchmessern nicht so übersichtlich wie bei Verwendung inkompressibler Schneidstrahlen. Lediglich die Querschnittsgeometrie der Fuge, gekennzeichnet durch B/S geht wieder direkt ein, die Dichte des Fugenstoffs umgekehrt proportional. Bemerkenswert ist, dass sowohl die Temperatur des Schneidstahls als auch die spezielle Gaskonstante im Nenner unter der Quadratwurzel auf die Grenze eingehen. Die spezielle Gaskonstante wiederum ist umgekehrt proportional zur molaren Masse des Schneidgases. "Schwere" Schneidgase wie Argon oder CO2 erhöhen somit die Grenze. Höhere Temperaturen verringern diese andererseits.
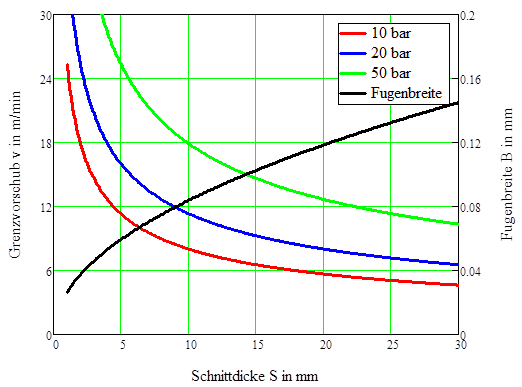
Die Grenzgeschwindigkeiten sind niedrig, da der engste Querschnitt im Düsenaustritt den Schneidstoffstrom begrenzt. Verdeutlicht wird der Verlauf der Grenzgeschwindigkeit über ein Berechnungsbeispiel, Bild (11). Dort sind die beim Schneiden üblichen Vordrücke von Schneidstrahlen aus Stickstoff eingegangen bei optimierten Fugenbreiten von Grundmode-CO2-Laserstrahlen.
Beispielsberechnung
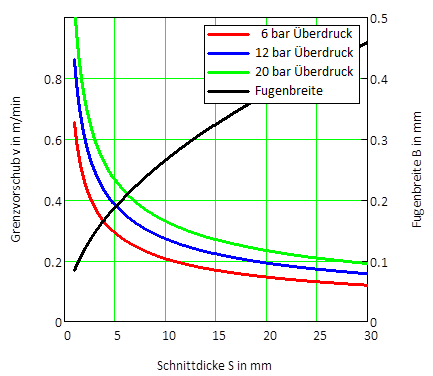
Im Vergleich dieser Berechnungen mit den in Schneidtabellen von Anlagenherstellern angegebenen Werten sind die berechneten Grenzgeschwindigkeiten deutlich niedriger als die in der Praxis erzielten. Die Ursache liegt darin, dass die Berechnungen für Schneidstrahlen gelten, deren Durchmesser an die Schnittfugenbreite angepasst sind. Die den Schneidtabellen zugrundeliegenden Schneiddüsen-Durchmesser sind etwa um einen Faktor fünf größer. Die Düsen sind keine Lavaldüsen, so dass der Schneidstrahl nach dem Austritt noch expandiert. Mit derart großen Durchmessern der Schneidstrahlen ist der Verbrauch von Schneidgasen wesentlich größer als bei Verwendung angepasster Düsen. Wo die Grenzen der Vorschubgeschwindigkeiten mit großen Schneidstrahldurchmessern liegt, wird im nächsten Schritt ermittelt.
1.1.2.2 Große Durchmesser kompressibler Schneidstrahlen
Die starke Begrenzung des Stoffstromes im Schneidstrahl aufgrund der Schallgeschwindigkeit im engsten Querschnitt der Schneiddüse kann durch Wahl eines großen Querschnitts am Düsenausgang überwunden werden.
Wie in der Behandlung inkompressibler Schneidstrahlen gilt auch hier, dass der Schneidstrahl-Strom mit Durchmessern, die deutlich größer sind als die Fugenbreite im Wesentlichen parallel zur Oberfläche des Schneidteils abgelenkt wird. Die Komponente seines Impulsvektors in Strahl-Strömungsrichtung beim Auftreffen auf die Oberfläche des Schneidteils geht gegen null. Aus dieser Impulsänderung baut sich der in die Fuge einwirkende Staudruck Pein auf. Somit kann der Raum oberhalb des Schneidteils als Raum als Raum mit dem Eingangs-Staudruck Pein betrachtet werden. Der Staudruck Pein treibt den fluidisierten Fugenstoff aus.
Mit diesem Ansatz ergibt sich für den austretenden Stoffstrom nach Bernoulli entsprechend Gleichung (3) die Austrittsgeschwindigkeit uaus
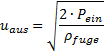 (63)
(63)
Der „Staudruck“ Pein ist zunächst noch unbekannt. Er ergibt sich aus den Gesetzen zur Lavaldüse. Eine Näherungslösung ist bekannt, so dass auf eine ausführlichere Herleitung verzichtet wird.
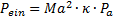 (64)
(64)
In dieser Gleichung ist Pa der bekannte Umgebungsdruck, siehe Bild 10. Mit Kenntnis von Pein und dem Festlegen der Schichtdicke des ausströmenden Fluids auf die Fugenbreite wird entsprechend der Argumentation zu den Gleichungen (42) bis (44) vorgegangen. Mit Gleichung (61) führen diese zur Grenzgeschwindigkeit beim Laserstrahlschneiden mit kompressiblen Schneidstrahlen großer Querschnitte, Gleichung (65)
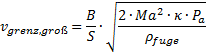 (65)
(65)
Die Machzahl ist aus Gleichung (50) bekannt, so dass sich die Grenzgeschwindigkeit für das Schneiden mit kompressiblen Schneidstrahlen großer Durchmesser unter Verwendung der üblich angegebenen Betriebsparameter in folgender Gleichung (66) dargestellt wird.
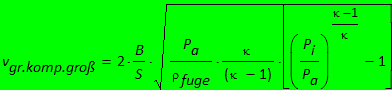 (66)
(66)
Der Einfluss der Betriebsparameter auf die Grenzgeschwindigkeit ist bei kompressiblen Schneidstrahlen mit großen Durchmessern nicht so übersichtlich wie bei Verwendung inkompressibler Schneidstrahlen großer Durchmesser. Lediglich die Querschnittsgeometrie der Fuge, gekennzeichnet durch B/S geht wieder direkt ein, die Dichte des Fugenstoffs im Nenner unter der Quadratwurzel. Bemerkenswert ist, dass die Dichte des Schneidstrahl-Stoffs nicht in die Grenze eingeht. Bei großen Durchmessern kompressibler Schneidstrahlen ist die Grenzgeschwindigkeit somit beinahe unabhängig von der Art des Schneidstahl-Stoffs. Ein geringer Beitrag resultiert aus den Unterschieden der Isentropenexponenten der verschiedenen Gasarten.
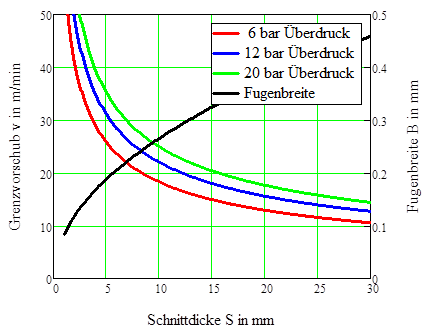
Die für große Durchmesser kompressibler Schneidstrahlen errechneten Grenzgeschwindigkeiten sind bei den üblichen für das Schneiden von Metallen gewählten Vordrücken hoch. Hingewiesen wird hier darauf, dass die Berechnungen nur für höhere Machzahlen gelten, das heißt für Vordrücke, die den Umgebungsdruck deutlich übersteigen.
1.1.2.3 Zusammenfassung der Ergebnisse zur Fugenbildung
mit kompressiblen Schneidstrahlen
Für die Vorschubgeschwindigkeit beim Laserstrahl-Schneiden existieren Obergrenzen, die auf der Tatsache beruhen, dass der Fugenstoff aus dem Bereich des Laserstrahls nach unten (also in Laserstrahl-Ausbreitungs-Richtung) aus der Schnittfuge ausgetrieben werden muss. Dies wurde mit Hilfe der Erhaltungssätze für Stoff, Energie und Impuls abgeleitet.
Eine Obergrenze beruht auf der Übertragung des Schneidstrahls auf den fluidisierten Fugenstoff. Diese Obergrenze ist unabhängig davon, ob das Fluid als Gas, Schmelze oder Gas-Schmelze-Gemisch vorliegt. Eine weitere beruht beim Schmelzschneiden auf der Dicke der sich bildenden Schmelzeschicht. Ist diese dünn, dann wird der Viskositäts-Einfluss den effektiven Austrag behindern. Ist diese dick, dann führt aufgrund der endlichen Wärmeleitfähigkeit die Temperaturdifferenz zwischen Einwirkbereich des Laserstrahls auf die Schmelze und festem Stoff zum Verdampfen der Schmelze. Somit wird der Schmelze Wärmeleistung entzogen. Der Schneidvorgang geht dann vom Laserstrahl-Schmelzschneiden über in das Laserstrahl-Sublimierschneiden. Über diese Schneidart lassen sich mit erhöhter Laserleistung immer höhere Schneidgeschwindigkeiten erzielen - bis dann letztendlich die Obergrenze aus der Impulsbilanz erreicht wird. Diese Obergrenze erhöht sich mit höheren Vordrücken über den Exponenten 1/2. Andererseits lassen einige Stoffarten nur geringe Vordrücke zu, so dass die Impulsbilanz die Schneidgeschwindigkeit begrenzt.
Wie nah sich diese Obergrenzen überhaupt annähern lassen, hängt von einer Vielzahl weiterer Bedingungen ab. Beispielsweise stellt sich die Frage, in wie weit der Schneidstrahl die Schnittfuge im Bereich der Schneidfront vollständig durchströmt und somit an den fluidisierten Fugenstoff ankoppelt oder auch die, unter welchen Bedingungen der Einfluss der Viskosität des fluidisierten Fugenstoffs vernachlässigbar ist.
↑ 1.1.3
Vergleich der Fugenbildung zwischen inkompressiblen
und kompressiblen Schneidstrahlen
Schneidstrahlen aus nahezu inkompressiblen Stoffen sind Flüssigkeiten wie beispielsweise Wasser. Flüssigkeiten weisen eine Dichte auf, die 103 bis 104 höhere ist als die von Gasen. Dementsprechend unterscheiden sich auch die Wirkungen beider Stoffströme, wenn sie gleiche Geschwindigkeit aufweisen. Andererseits erfordern dichte Fluide einen höheren Vordruck in der Schneiddüse als die weniger dichten, wenn sie gleiche Strömungsgeschwindigkeit aufweisen sollen. Die beiden Einflüsse heben sich somit auf. So sollte das Schneiden mit einem inkompressiblen Stoff zum gleichen Ergebnis führen wie mit einem kompressiblen, wenn die anderen Parameter die gleichen sind.
Das ist jedoch nicht der Fall wenn die Strömungsgeschwindigkeit eines Gases die Schallgeschwindigkeit überschreitet und mit dieser Geschwindigkeit auf den Fugenstoff einwirkt. In dem Fall treten Verdichtungstöße mit irreversiblen Zustandsänderungen auf, wodurch die Übertragung von Impuls und kinetischer Energie auf den Fugenstoff verringert wird.
Ein Schneidstrahl erreicht Überschallgeschwindigkeit durch Expansion nach dem engsten Düsenquerschnitt. Das bedeutet, dass der Stoffstrom eines Strahls durch den engsten Düsenquerschnitt bestimmt wird und nicht nur durch die Fugenbreite. Die Düse sperrt sozusagen im engsten Querschnitt. Damit wird auch die Schneidgeschwindigkeit deutlich kleiner als die aus einem großen Strahlquerschnitt resultierende, vergleiche Bild 12 mit Bild 13. Zum Vergleich der Grenz-Schneidgeschwindigkeiten zwischen inkompressibler und kompressiblen Schneidstrahlen werden daher die Ergebnisse für große Strahlquerschnitte betrachtet.
Eine Analyse der Gleichungen (46) und (66) könnte die Unterschiede in der Auswirkung zeigen. Gleichung (66) ist jedoch unübersichtlich. Sie gilt zudem nur für höhere Machzahlen des Schneidstrahls, also mit höheren Vordrücken. Der Übersichtlichkeit wegen wird das Verhältnis der Schneidgeschwindigkeiten für Fälle gebildet und das Ergebnis in einem Graphen diskutiert, Bild 14.
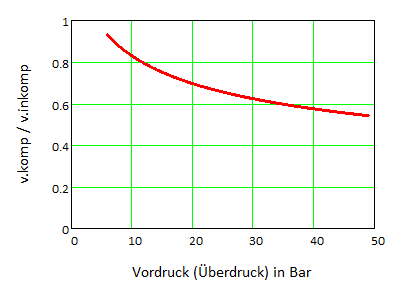
Das Verhältnis der Grenzgeschwindigkeiten zwischen kompressiblen Schneidstrahlen zu inkompressiblen Schneidstrahlen ist bis zum kritischen Vordruck etwa 1. Der kritische Vordruck ist in der Umgebung mit dem Druck 1 bar etwa bei einem Überdruck in der Düse von 1 bar (also bei etwa 2 bar absolut) erreicht.
Der Vergleich umfasst den Vordruck-Bereich zwischen 6 bar und 50 bar Überdruck. 6 bar wird beim Schneiden mit Stickstoff für kleinere Schnittdicken gewählt; 50 bar sind in inkompressiblen Fluiden ohne größeren Aufwand erreichbar.
Wenn kompressible Schneidstrahlen verwendet werden, dann verringert sich die höchstmögliche Schneidgeschwindigkeit bis auf etwa die Hälfte derjenigen, die mit inkompressiblen Schneidstrahlen erreichbar ist. Die Ursache dieser Verringerung liegt in dem Phänomen, dass im Stoß von Überschallströmungen irreversible Verluste auftreten. Diese werden in der Näherungslösung Gleichung (55) erfasst und gehen somit in das Ergebnis Bild 14 ein.
↑ 1.2 Einbringen des Schneidstrahls in die Schnittfuge
In konventionellen Schneidanlagen wird ein Schneidstrahl aus Gas in Düsenkörpern wie in Bild (3) oder Bild (10) aufgebaut. Die den Schneidstrahlquerschnitt festlegenden Durchmesser der Öffnungen sind hierin deutlich größer als die Schnittfugenbreite; denn ein fokussierter Lasestrahl passt nicht durch angepasste Düsen, Bild (15). Daher werden die Berechnungen für große Schneidstrahlquerschnitte die Ergebnisse aus den Anwendungen besser beschreiben als die für angepasste Durchmesser.
Beim Vergleich dieser Berechnungs-Ergebnisse für große Schneidstahl-Durchmesser mit den Angaben in Schneidtabellen zeigt sich, dass die aus den Erhaltungssätzen gegebenen physikalischen Obergrenzen der Schneidgeschwindigkeit mit konventionellen Laser-Schneidanlagen nicht erreicht werden. Das bedeutet, dass Energie und Impuls des Schneidstrahls nicht maximal an den Fugenstoff übertragen werden. Ursachen hierfür sind darin zu sehen, dass der Schneidstrahl nicht wie gewünscht in der Schnittfuge wirkt. Das wird deutlich in der Beschreibung von Schnittflächen. Eine Besonderheit ist die Riefenbildung (Rillenbildung). An Schnittflächen von dickeren Schneidteilen fällt auf, dass die Rillen von der Oberseite her in den ersten Millimetern gleichmäßig parallel zur Laserstrahl-Achse verlaufen. Dann weichen sie nach hinten ab, also entgegen der Schneidvorschubrichtung, Bild (16). Der untere Bereich wirkt ausgewaschen. Ein leichter, fest anhaftender Schneidbart wurde entfernt.

Schnittfugenbreite B = 0,4 mm; 2,5-kW CO2-Industrielaser mit KI = 0,03 mm; Schneidstrahl Stickstoff; Vordruck Pi = 20 bar; Düsendurchmesser 2 mm; Schneidvorschunb v = 0,5 m/min
Zum Verstehen der Ursachen dieses Ergebnisses wurde das Verhalten von Schneidstrahlen beim Eintereten in die Schnittfuge auf verschiedenen Wegen untersucht. Dies Untersuchungen werden hier kurz als Bildserie dargestellt, da ein genaueres Eingehen den Rahmen des Kapitels zur Fugenbildung sprengen würde.
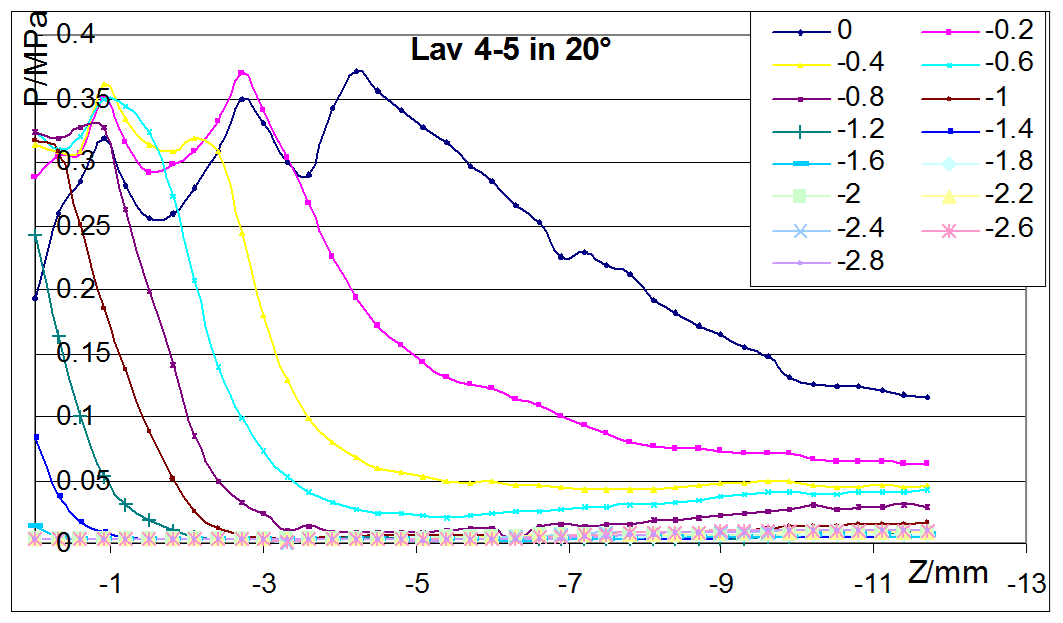
Die ersten Untersuchungen befassten sich mit dem Schneidstrahl aus konventionellen, also nicht angepassten, Schneiddüsen. Hier wurde mittels Pitot-Sonden die Strömung in der Schneidstrahlachse mit und ohne Spalt vermessen. Dabei wurden im Verlauf des Freistrahls von der Mündung im Abstand von etwa 2 mm abwechselnd Minima und Maxima des Staudrucks beobachtet. Diese Erscheinung wird in Schlierenbilder deutlich, Bild 17. Hier wird der Unterschied zwischen dem Strahl aus einer Mündung gegenüber einer angepassten Lavaldüse deutlich. Der Freistrahl aus der angepassten Lavaldüse verläuft ohne Knoten, der aus der Mündung zeigt deutlich eine Nachexpansion zu einem Bauch und anschließender Kontraktion in einen Knoten. Weiter Bäuche mit Knoten wechseln ab.
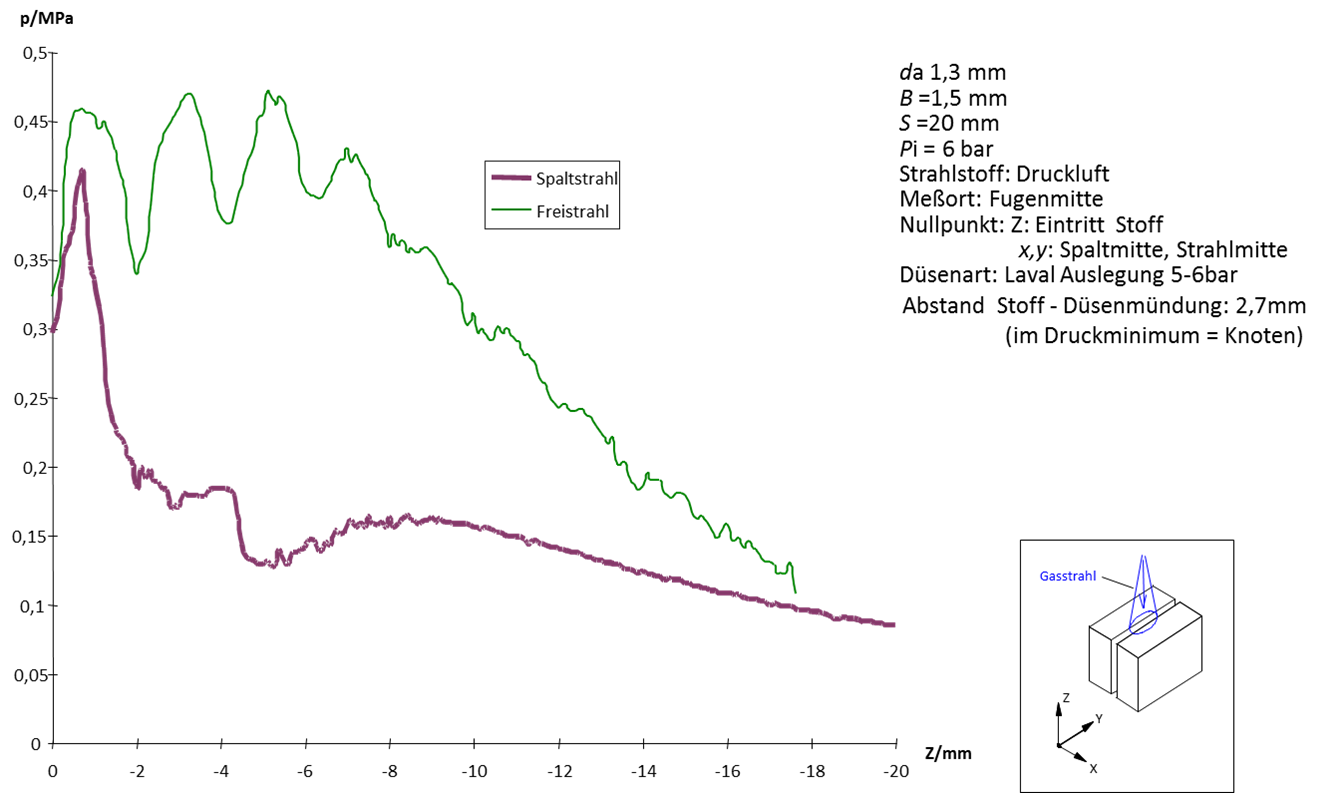
Liegt die Oberfläche des Schneidteils im Staudruck-Maximum des Schneidstrahls (entsprechend der Knotenposition), dann sinkt der Staudruck innerhalb des Spaltes nach einem mm Eindringtiefe abrupt ab, um dann auf niedrigem Pegel bis an die Spaltunterseite weiter zu verlaufen,Bild 18 [5]. Befindet die Oberfläche im Staudruck-Maximum des Freistrahls, dann folgt der Staudruckverlauf im Spalt etwa dem des Freistrahls, Bild 19.[5] Für die Praxis des Laserstrahl-Schneidens bedeutet dies, dass der Mündungsabstand zur Schneidteil-Oberseite in engen Grenzen eingehalten werden sollte.
Ähnliche Messungen wurden auch in einem Spalt mit einseitigen Begrenzung zur Darstellung der Schneidfront durchgeführt. Diese zeigten gleiche Erscheinungen dann, wenn der Schneidsrahl parallel zur Schneidfront in den Spalt eintrat. Bei Neigung des Strahls derart, dass er auf die Schneidfront trifft, dringt der Schneidstrahl-Strom mit hoher Geschwindigkeit (hohem Staudruck) noch tiefer entlang der Schneidfront in den Spalt, Bild 20. Die Strömung ist an der Schneidfront konzentriert; sie weitet wenig auf.
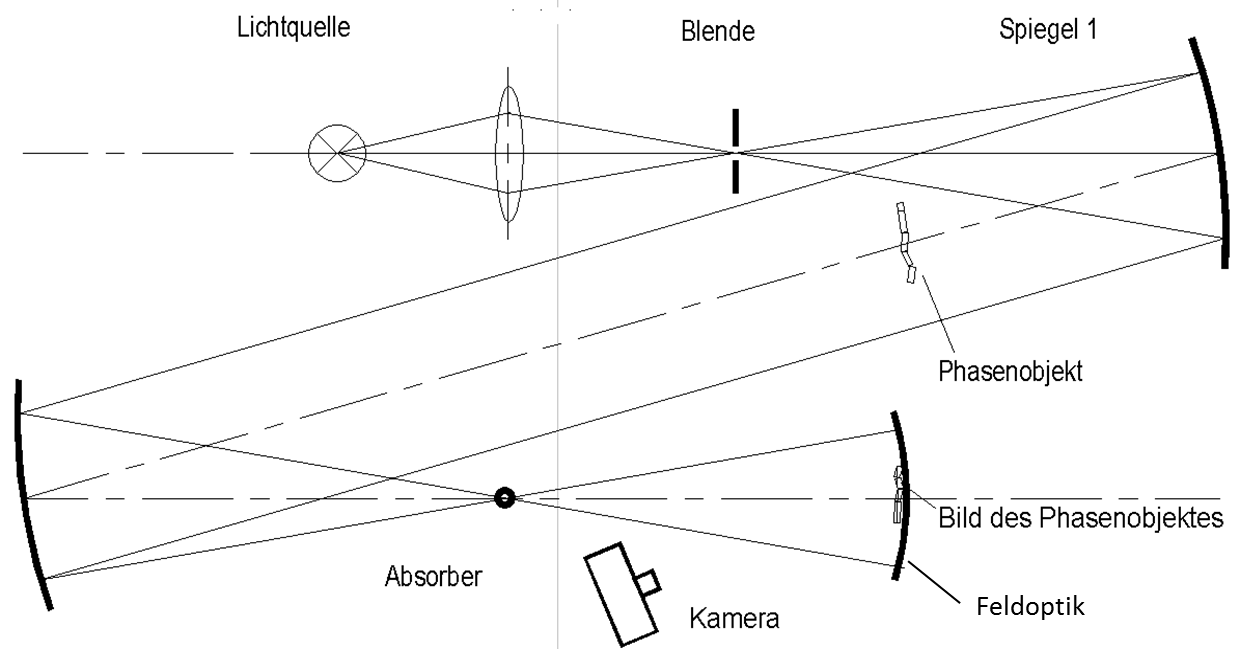
In den Untersuchungen mit der Staudrucksonde war der Einfluss der Sonde auf den Strömungsverlauf nicht auszuschließen. Aus diesem Grund wurden die Experimente durch schlierenoptische Untersuchungen in einem schlierenoptischen Aufbau, Bild 21, ergänzt. Als Schneidspalt diente ein tranparentes Modell aus Glas, Bild 22. Der Schneidstrahlverlauf in den schlierenoptischen Bildern bestätigt die Messungen über die Pitotsonde, Bild 23.
Wie sich ein Schneidstrahl auf die Strömung eines Fluids an der Schneidfront auswirkt, wurde in weiteren Modellversuchen geprüft. Hierzu wurde Wasser als Modellschmelze gewählt und in ein Schnittfugenmodell durch Bohrungen in die Scheidfront eingebracht, Bild 24, und die Wirkung des Schneistrahls von der Seite beobachtet. Hier zeigt sich, dass der Fluidstrom schon in gerigen Abständen von der Oberseite des Schneidmodells in nach hinten den Spalt strömt, Bild 25, wenn der Schneidstrahl parallel zur Schneidfront eingebracht wird. Bei stechend geneigtem Schneidstrahl strömt die Modellschmelze noch in größeren Tiefen entlang der Schneidfront, Bild 26.
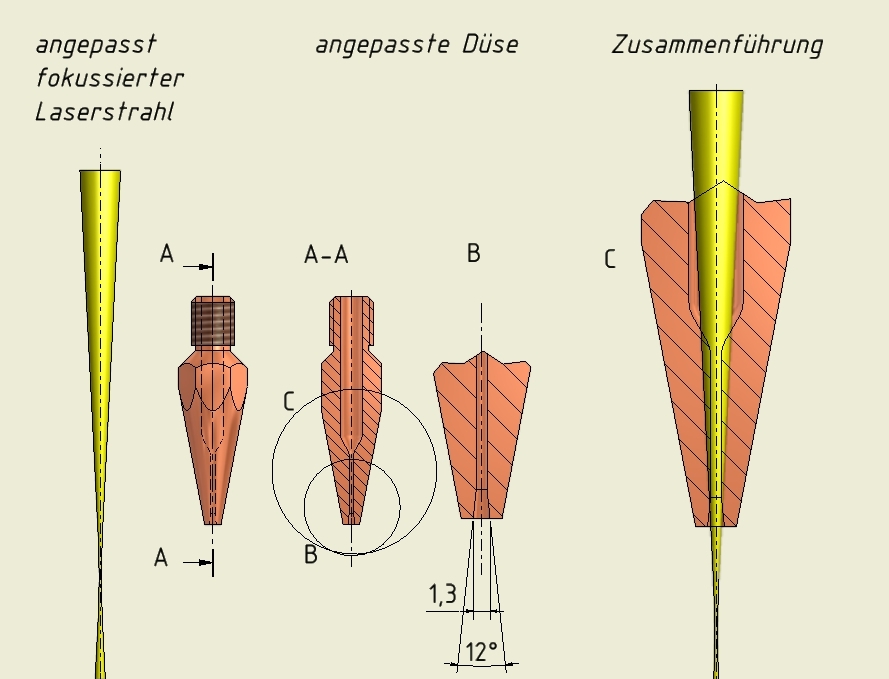
Diese Untersuchungen zeigten, dass eine nachlaufender Schneidstrahl in stechender Anordnung zum Austragen des Fugenstoffs Vorteile bringen könnte. Als weiterer Vorteil kann gesehen werden, dass in einer Schneidanordnung mit nachlaufendem Schneidstrahl auf transparente Opiken verzichtet werden kann. Transparente Optiken verformen sich bei hoher Belastung durch den Laserstrahl und sind empfindlich gegen Verschmutzung. Einfache robuste Spiegeloptiken, die beim Laserstrahl-Schweißen mit Hochleistungslasern die Regel sind, können Verwendung finden. Zudem ist der Schneidstrahl frei formbar, Bild 27. Sein Durchmesser kann beliebig gewählt werden. Eine angepasste Lavaldüse lässt sich einsetzen. Angepasste Lavaldüsen sind für das autogene Brennschneiden weit entwickelt und gehören dort zum Standard.
Mit einer derartigen Anordnung wurden erste Versuche erfolgreich begonnen, Bild 28 und Bild 29
Bildserie

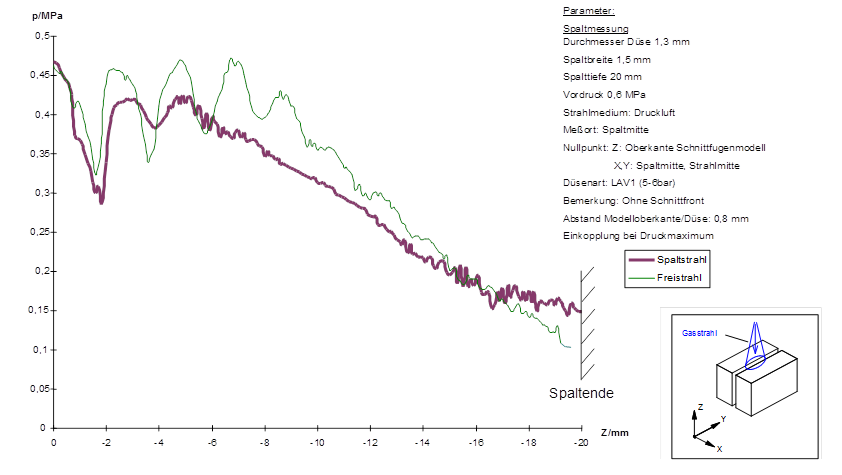


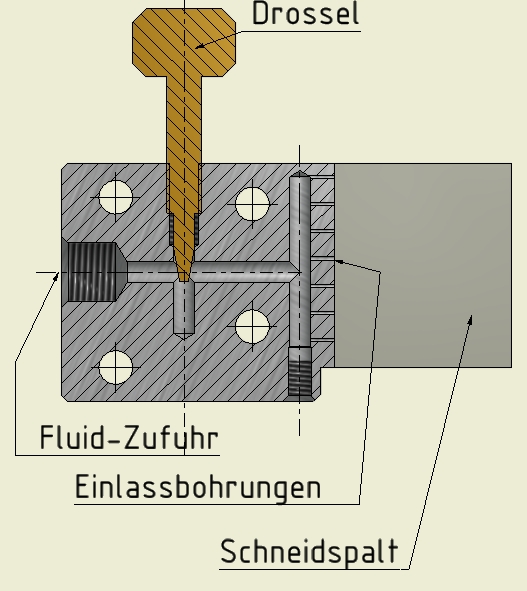

Strömungsverlauf eines Wasserstroms als Modell-Schmelze. Der Schneidstral tritt parallel zur Schneidfront an der Schneidfront in den Spalt ein. Volumenstrom Wasser: entsprechend Schneidvorschub v = 2 m/min; Düsenabstand 1 mm; Vordruck 3 bar

Strömungsverlauf eines Wasserstroms als Modell-Schmelze. Der Schneidstral tritt in einem Winkel von 17° zur Schneidfront stechend in den Spalt ein. Volumenstrom Wasser: entsprechend Schneidvorschub v = 2 m/min; Düsenabstand 1 mm; Vordruck 3 bar

und mit nachlaufender Düse (rechts)


P = 2 kW; v = 1,1 m/min; Stickstoff 6 bar;
Schnitt mit fliegendem Anschnitt; Aufnahme im Moment des Schneidendes, das abgeschnittene Teil fällt
Die Bildserie soll im Wesentlichen dazu anregen, auf dem Gebiet des Optimierens von Schneidanordnungen weiter zu forschen und Schneidköpfe zu entwickeln.
↑ 2 Erwärmung
Die Ausführungen werden zurückgestellt bis das Kapitel "Wechselwirkung" fertiggestellt ist
Referenzen
[1] Als Beispiel dient hier das schon ältere DIN-Taschenbuch "Fertigungsverfahren 2", im Beuth-Verlag erschienen 1986
[2] Der Vorgang wird unter "Abtragen" behandelt
[3] Der Vorgang wird unter "Abtragen" behandelt
[4] Wegen der Verwechslungsgefahr mit den Symbolen für Druck und Impuls wird hier L anstatt P gewählt.
[5] Aus Arbeiten zur Dissertation Thomas Schüning 2002, "Verbesserung der Schnittfugenbildung beim Laserstrahlschneiden durch Erhöhung der Impulsübertragung aus Schneidstrahlen"